دوست خوبم سلام!
به آموزش فصل ششم ریاضی دهم خوش اومدین! فصل ششم ریاضی دهم در مورد شمارش اعداد بدون شمارش ، مفهوم فاکتوریل ، جایگشت حروف و اعداد ، فرمول ترکیب و ترتیب هستش که تمامی این مفاهیم بصورت پله ای از ساده به سخت در قالب مثال هایی کاملا شفاف و ساده شرح داده شده ، خوبه که بدونین از این مبحث همیشه توی کنکور سراسری یک تست مطرح میشه که عموم دانش آموزان حتی با داشتن اطلاعات در حد امتحانات کلاسی از پس حلش بر میان ، پس این فصل رو جدی بگیرین . تنها مشکل این فصل شبیه بودن مفاهیم هستش که سعی کردیم مطالب رو جدا جدا توضیح بدیم تا یک دید جامع نسبت به فصل پیدا کنین ، در دوره آموزشی فصل ششم ریاضی دهم تمامی تمرینات ، مثال ها و فعالیت های کتاب درسی بصورت گام به گام با شیوه حل مساله براتون حل شده ، پس نگرانی بابت تمرینات کتاب درسی هم ندارین ،
خیلی خوب وقت رو تلف نکنین و برای مشاهده درسنامه های رایگان فصل ششم ریاضی دهم به پایین همین صفحه مراجعه کنین.
فصل ششم ریاضی دهم – بخش اول – جایگشت
خلاصه فصل : توی این فصل آموزشی می خوایم با مبانی و اصول اولیه اصل ضرب و اصل جمع آشنا بشیم و حالت های مختلف انتخاب کردن رو یاد بگیرین ، بمرور مطالب و انتخاب هایی که انجام میشه پیشرفته تر میشه و فرمول های مهم و اساسی احتمال رو معرفی میکنیم….
درسنامه اول
هدف درسنامه : بررسی اصل جمع و اصل ضرب در شمارش اعداد
خلاصه درسنامه : تو درسنامه اول در مورد اصل ضرب و اصل جمع با شما صحبت میکنیم.
- اصل جمع :
اگه کاری رو بشه به دو روش انجام داد به طوری که توی روش اول n انتخاب و در روش دوم m انتخاب وجود داشته باشه در کل m+n انتخاب وجود خواهد داشت. ( نحوه تشخیصش به این صورته که بین کارها از کلمه یا میشه استفاده کرد هرجایی گفتید مثلا این کار انجام بشه یا اون کار انجام بشه در حقیقت با اصل جمع روبرو شدین ) - اصل ضرب :
اگه انجام کاری شامل دو مرحله باشه به نحوی که مرحله اول شامل n روش و هر روش خودش شامل m روش دیگه باشه ( یعنی m زیر روش داشته باشه و به زیرشاخه تبدیل بشه ) در کل کار مورد نظر رو به n × m روش مختلف میشه انجامش داد. ( نحوه تشخیصش به این صورته که بین روش های مختلف کلمه ” و ” استفاده میشه )
مثال : شخصی ۵ کفش ، ۴ شلوار و ۲ پیراهن مختلف دارد به چند شکل متفاوت می تواند هر سه تای آنها را باهم بپوشد.
۵ * ۴ * ۲ = ۴۰ به ۴۰ روش مختلف میتواند هر سه تای آنها را بپوشد
مثال بالا نمونه ساده از تحلیل مسائل اصل ضرب و اصل جمع بود برای آشنایی بیشتر درسنامه اول این قسمت را مشاهده کنید.
درسنامه دوم
هدف درسنامه : بررسی مفهوم جایگشت حروف
خلاصه درسنامه : تو درسنامه دوم درباره ساخت کلمات و حروف با تکرار و بدون تکرار ( جایگشت ) صحبت میکینم ، بعد از اتمام این درس یاد میگیرید که مثلا با حروف کلمه ی ” بادرنگ ” چند کمله ی ۴ حرفی با تکرار و یا بدون تکرار ساخت.
نکته : واژه جایگشت در هر سوالی مطرح شد به این معنی هستش که تکرار حروف مجاز نیستش
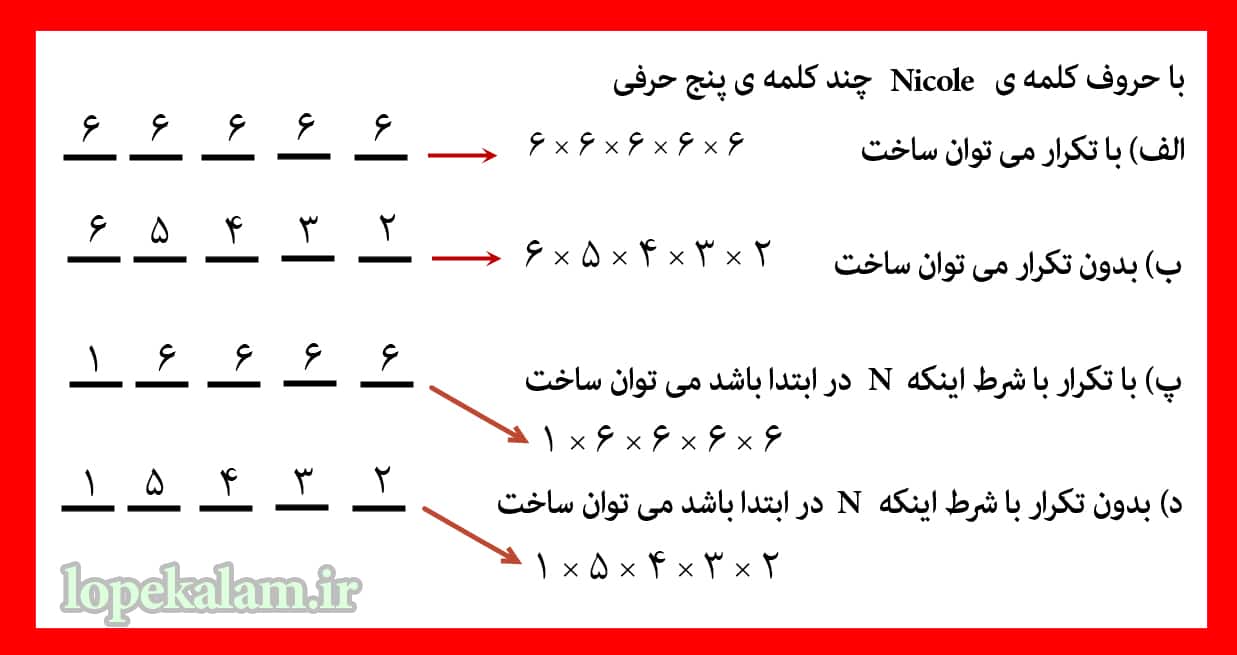
کلا در تحلیل مسائل جایگشت ( بدون تکرار ) و یا با تکرار حروف و ساختن کلمه ها ، به تعدادی که سوال از ما خواسته جایگاه در نظر می گیریم و هر جایگاه رو با تعداد حروفی که داریم پر میکنیم اگه تکرار حروف مجاز نباشه بعد از پر شدن هر خونه یکی از تعداد کل کم میشه بصورت مثال کلمه ی ” بادرنگ ” در مجموع از شش حرف ” ب آ د ر ن گ ” ساخته شده که اگه قرار باشه باهاش کلمه های ۴ حرفی بسازیم توی خونه اول میشه ۶ حرف قرار داد و توی خونه بعدی میشه ۵ حرف قرار داد و همینطور توی خونه بعدی ۳ حرف و در نهایت توی خونه ی آخر میشه ۲ حرف قرار داد در نهایت تمامی این عدد ها توی همدیگه ضرب میشن برای درک بهتر آنچه گفته شد توصیه میکنم که حتما درسنامه زیر رو مشاهده و دانلود کنین تا درک بهتری از جایگشت حروف بدست بیارین.
درسنامه سوم
هدف درسنامه : ترکیب حروف با شرط های خاص
خلاصه درسنامه : گاهی هنگام ترکیب کلمات و حروف یک سری شرایطی گذاشته میشه که تو درسنامه سوم در مورد این شرایط خاص صحبت میکنیم یعنی توی بعضی سوالات قید میشه که مثلا فلان حرف حتما توی خونه اول قرار بگیره یا مثلا حتما هنگام ترکیب حروف ابتدا کلمات صدا دار قرار داده بشه ، تو این درسنامه یاد میگیرید که تو اینجور سوالات چجوری عمل کنین و مسائل اینشکلی رو چه شکلی تحلیل کنین ، به یک مثال دقت کنید تا درکتون از این درسنامه بهتر بشه.
مثال : با کلمه ی ” jacek ” چند کلمه ی ۵ حرفی بدون تکرار می توان ساخت به نحوی که حرف j در آغاز و حرف K در انتها قرار داشته باشه ؟
جواب : با توجه به اینکه درون سوال قید شده که حرف j در خانه اول قرار بگیره بنابراین خونه ی اول فقط یک حالت به خودش میگیره و همچنین خونه ی آخر که جایگاه k هستش یک حالت میگیره سه حرف باقی مونده به ترتیب ۳ ، ۲ و یک حالت به خودش اختصاص میده و جواب نهایی میشه حاصل ضرب این حالت های مختلف یعنی میشه ۱ × ۳ × ۲ × ۱ × ۱ که در کل میشه ۶ حالت مختلف ، دقت کنین که عدد ۱ اولی و عدد ۱ آخری مربوط به شرط خاص ” j ” و ” k ” هستش .
درسنامه چهارم
هدف درسنامه : ترکیب اعداد با وجود عدد صفر
خلاصه درسنامه : تو این درسنامه قراره که ترکیب اعداد رو بررسی کنیم ، فرق این درسنامه و درسنامه قبلی تو این هستش که رقم اول هیچ عددی نمیتونه صفر باشه بنابراین همیشه دقت کنین که توی تحلیل هاتون خونه اول نمیتونه صفر باشه و یک حالت از کل حالت ها کم میشه ، در ضمن چنتا نکته هستش که به درک این درسنامه بیشتر کمکه میکنه که در زیر دسته بندی کردیمش
- به اعدادی زوچ گفته میشه که عدد یکان آنها ۰ یا ۲ یا ۴ یا ۶ یا ۸ باشه
- به اعدادی فرد گفته میشه که عدد یکان آنها ۱ ، ۳ ، ۵ ، ۷ ، ۹ باشه
- به عددی مضرب ۵ گفته میشه که رقم آخر اون ۰ یا ۵ باشه
- به عددی مضرب ۳ گفته میشه که مجموع ارقامش بر ۳ بخش پذیر باشه
- به عددی مضرب ۶ گفته میشه که هم بر ۳ و هم بر ۲ بخش پذیر باشه
درسنامه پنجم
هدف درسنامه : ترکیب اعداد فرد
خلاصه درسنامه : تو این درسنامه به صورت ویژه در مورد ترکیب اعداد فرد صحبت میکنیم. بصورت مثال با اعداد ۱۳۴۰۹ چند عدد فرد پنج رقمی میتوان ساخت.
اول از همه دقت کنید که عدد ۱۳۴۰۹ در مجموع ۵ رقم مجزا داره
برای حل این مدل سوالات باید دقت کنیم که عددی فرد است که رقم اخر اون فرد باشد بنابراین تو خونه ی آخر فقط عدد ۱ ، ۳ و ۹ میشه نوشت که یعنی خونه آخری میشه ۳ حالت و دقت بشه که عدد اولی نمیتونه صفر باشه پس یک حالت از کل حالت ها کم میشه در واقع ۴ حالت براش باقی میمونه ، اما دو تا خونه وسطی هیچ شرطی ندارن پس بنابراین کل ۵ حالت رو قبول میکنن ، دقت کنین همیشه برای حل سوالات جاگذاری ارقام رو با خونه هایی شروع کنین که شرایط خاصی بر روی اونها حاکم هستش. پس در کل به تعداد ۳۰۰ حالت مختلف میشه عدد فرد ساخت.
۴ × ۵ × ۵ × ۳ = ۳۰۰
درسنام ششم
هدف درسنامه : ترکیب اعداد مضارب ۵
خلاصه درسنامه : تو این درسنامه در مورد ترکیب اعداد مضارب ۵ صحبت میکنیم. بصورت مثال با اعداد ۱۳۴۰ چند عدد زوج چهار رقمی میتوان ساخت؟ ( تکرار ارقام مجاز است )
همونطوری که قبلا تو همین متن اشاره کردیم عددی مضرب ۵ هستش که رقم آخر اون صفر یا پنچ باشه ، بنابراین رقم صفر باید توی خونه ی آخری قرار بگیره و خونه ی آخر میشه یک حالت ، اما تو خونه ی اول نمی تونه عدد صفر قرار بگیره چون صفر در اولین رقم بی معنی هستش پس خونه ی اول میشه ۳ حالت ، اما دو تا خونه وسطی هیچ شرط خاصی ندارن و هر کدوم ۴ حالت رو به خودشون اختصاص میدن بنابراین در مچموع با ۴۸ حالت مختلف میشه اعداد مضرب ۵ ساخت.
۳ × ۴ × ۴ ×۱ = ۴۸ حالت
درسنامه هفتم
هدف درسنامه : جایگشت اعداد زوج
خلاصه درسنامه : این درسنامه در مورد جایگشت اعداد زوج هستش. بصورت مثال با اعداد ۱۲۳۴۵۶۷۸ چند عدد زوج پنج رقمی می توان ساخت. ( تکرار ارقام مجاز نیست )
کاملا مشخصه که عددی زوج هستش که رقم آخر اون زوج باشه ، پس تو مثال بالا ارقام ۲ ، ۴ ، ۶ و ۸ میتونن توی خونه ی اخر قرار بگیرن که میشن ۴ حالت و اما از اونجایی که تکرار ارقام مجاز نیستش توی خونه اول یک حالت از کل حالت ها کم میشه و در واقع میشه ۷ حالت و در خونه ی دوم ، ۲ حالت کم میشه و میشه ۶ حالت به همین ترتیب در خونه ی سوم ، ۳ حالت کم میشه و میشه ۵ حالت و این روند ادامه داره تو خونه بعدی ۴ حالت میشه عدد جاگذاری کرد.
۷ × ۶ × ۵ × ۴ × ۱ = ۸۴۰
درسنامه هشتم
هدف درسنامه : جایگشت حروف به هم چسبیده
خلاصه درسنامه : این درسنامه در مورد جایگشت اعداد خاص هستش بصورت مثال در کلمه ” گل پیرا ” کلمات ” پ ی ر ا ” کنار هم قرار بگیرند. که توی متن درسنامه مثال هایی با این موضوع تدریس شده است.
بخش دوم فصل – فاکتوریل – ترکیب و ترتیب در ریاضی
خلاصه مطالب :
- آشنایی با مفهوم فاکتوریل
- فرمول های انتخاب ( ترکیب ، ترتیب )
- مثال های بیشتر فرمول های ترتیب و ترکیب
- بررسی مفهوم ” یا ” ، ” و ” در انتخاب اشیاء
- بررسی مفهوم ” حداقل ” و ” حداکثر ” در انتخاب اشیاء
- زیر مجموعه های یک مجموعه
- جایگشت حروف به هم چسبیده
خلاصه مطالب : به بخش دوم فصل ششم رسیدیم و تو این بخش با مفهوم جدیدی تحت عنوان فاکتوریل آشنا میشین و غیر از اون با نحوه انتخاب کردن حالت های مختلف آشنا میشین…
درسنامه اول
هدف درسنامه : آشنایی با مفهوم فاکتوریل
خلاصه درسنامه : تو درسنامه اول در مورد مفاهیم فاکتوریل با شما صحبت میکنیم ، بصورت خیلی ساده معنی فاکتوریل به این صورت هستش که یک عدد رو از خودش شروع به ضرب کردن کن تا جایی که به یک برسی و دقت کنین که فاکتوریل یک عدد برای اعداد طبعی تعریف میشه و فرمولش به شکل زیر هست.
n! = n × ( n – 1 ) × ( n – 2 ) × ( n – 3 ) × ….. × ۱
مثال : !۶ یعنی ۶ ضربدر ۵ ضربدر ۴ ضربدر ۳ ضربدر ۲ ضربدر ۱
مثال : !۴ یعنی ۴ ضربدر ۳ ضربدر ۲ ضربدر ۱
توجه توجه : !۰ طیق تعریف برابر یک می شود.
توجه توجه : !۱ طبق تعریف برابر یک می شود.
۰! = ۱
۱! = ۱
برای درک بهتر مفهوم فاکتوریل و مشاهده مثال های بیشتر درسنامه زیر رو ببینید.
برای دانلود درسنامه فوق با کیفت خوب بر روی << اینجا >> کلیک کنید.
برای دانلود درسنامه فوق با کیفیت معمولی ( حجم کمتر ) بر روی << اینجا >> کلیک کنید.
درسنام دوم
هدف درسنامه : فرمول های انتخاب ( ترکیب ، ترتیب )
خلاصه درسنامه : تو درسنامه دوم میخوایم در مورد انواع انتخاب صحبت کنیم و فرمول هاشو بیان کنیم در حالت کلی ما دو دسته انتخاب داریم ، دسته اول ترتیب انتخاب کردن مهم نیستش و بصورت خلاصه به این حالت میگیم ” ترکیب ” و دسته دوم ترتیب انتخاب کردن مهم هستش که تو این حالت بصورت خلاصه بهش میگیم ” ترتیب “
- ترکیب
همونطوری که اشاره کردم تو این دسته ترتیب انتخاب کردن اهمیت ندره مثلا اگه قراره که از بین ۷ دانش آموز تجربی و ۵ دانش آموز ریاضی ۵ نفر رو انتخاب کنیم که ۳ نفر تجربی و ۲ نفر ریاضی باشه تو این انتخاب برای ما مهم نیستش که نفر اول تجربی باشه یا نفر دوم یا نفر سوم … فقط اون چیزی که مهمه این هستش که ۳ نفر تجربی و ۲ نفر ریاضی انتخاب بشن و اصلا اهمیتی نداره که دانش آموز تجربی یا ریاضی انتخاب شده چندمین انتخاب ما هستش ، پس تو این حالت ها میریم سراغ فرمول ترکیب . - ترتیب
برخلاف حالت قبلی توی این مدل انتخاب کردن برای ما اهمیت داره که ترتیب انتخاب کردن به چه شکلی هستش ، البته این نکته رو هم بگم معمولا زمانی که ترتیب انتخاب کردن مهم هستش بجای استفاده از فرمول ترتیت بصورت دستی و با کشیدن فلش و نمودار و … سوال رو تحلیل میکنیم و کمتر از فرمول ترتیب استفاده میکنیم. بصورت مثال از بین ۵ مهره سیاه و ۴ مهره سفید میخوایم ۳ مهره انتخاب کنیم به نحوی که مهره اول سفید مهره وسط سیاه و مهره آخر سفید باشه ، خوب همونطوری که دیدید توی این سوال دقیقا قید شده که مهره اول سفید باشه تو اینجور سوالات که بیشتر توی دوازدهم بررسی میکنیمش و اینجا فقط مفهومش رو بیان کردیم دیگه نمیشه ار فرمول ترکیب استفاده کرد.

درسنامه سوم
هدف درسنامه : مثال های بیشتر فرمول های ترتیب و ترکیب
خلاصه درسنامه : تو این درسنامه مثال های متنوعی از فرمول های ترکیب و ترتیب براتون حل میکنیم.
- سوالاتی که توی اونها در مورد انتخاب منشی ، رییس ، معاون و … صحبت میشه باید از فرمول ترتیب استفاده کرد. همچنین چیدن کتاب در ققسه و اول دوم و سوم شدن در مسابقات و … فرمول ترتیب باید استفاده کرد.
- سوالاتی که توی اونها در مورد انتخاب نقاط روی دایره و مشخص کردن زیر مجموعه ها ، انتخاب نقاط جهت تشکیل مثلث و در حالت کلی انتخاب بدون قید و شرط باید از فرمول ترکیب استفاده کرد.
مثال : از بین ۶ دانش آموز به چند طریق می توان ۴ نفر را برای شرکت در یک تیم کوهنوردی انتخاب کرد؟
از آنجایی که درون سوال برای انتخاب این ۴ نفر هیچ نوع قید و شرطی گذاشته نشده است بنابراین باید از فرمول ترکیب استفاده کرد.
c( 6 , 4 ) = 6! / 4! 2! = ۱۵ یعنی به ۱۵ حالت مختلف میشه این ۴ نفر رو انتخاب کرد
درسنامه چهارم
هدف درسنامه : بررسی مفهوم ” یا ” ، ” و ” در انتخاب اشیاء
خلاصه درسنامه : تو درسنامه چهارم انتخاب رو با شرایط خاص بررسی میکنیم و شروطی که بررسی میکنیم به دو کلی دسته تقسیم بندی میشه
- شروطی که توی اونها از کلمه ” یا ” استفاده میشه و معنی جمع کردن حالت ها رو میده
- شروطی که توی اونها از کلمه ” و ” استفده میشه و معنی ضرب کردن حالت ها رو میده
مثال : از میان ۵ دانش آموز دهمی و ۴ دانش آموز یازدهمی به چند طریق می توان یک کمیته ۵ نفره تشکیل داد به طوری که ۳ دانش آموز دهمی و ۲ دانش آموز یازدهمی باشد.
خوب همونطوری که میبینید بین انتخاب های سوال ، یعنی انتخاب ۳ نفر دهمی به علاوه ی ۲ نفر یازدهم از کلمه ی ” و ” استفاده شده است بنابراین حالت های صورت سوال را باید در همدیگر ضرب کرد. پس ما قراره از بین ۵ دانش آموز دهمی ۳ نفر همچنین از میان ۴ دانش آموز یازدهم ۲ نفر رو انتخاب کنیم و این انتخاب ها در همدیگر ضرب می شوند.
C( 5 , 3 ) × C( 4 , 2 ) = ۱۰ × ۶ = ۶۰
درسنامه پنجم
هدف درسنامه : بررسی مفهوم ” حداقل ” و ” حداکثر ” در انتخاب اشیاء
خلاصه درسنامه : خوب تو درسنامه های قبلی در مورد انتخاب با شما عزیزان صحبت کردیم تو درسنامه پنجم در مورد مفهوم حداقل و حداکثر صحبت میکنیم. برای درک بهتر فرض کنید که ۸ دانش آموز داریم و میخوایم از بین این دانش آموزان انتخابی رو انجام بدیم به این نحو که گفته بشه …
- مطلوب است حداقل ۵ نفر انتخاب بشه
توی این حالت وقتی گفته میشه که حداقل ۵ نفر انتخاب بشه یعنی به این معنی هستش که یا ۵ نفر انتخاب بشه یا بیشتر انتخاب بشه ، پس توی این مثالی که زدیم یعنی ۵ ، ۶ ، ۷ ، ۸ یا ۹ نفر انتخاب بشه یعنی همونطوری که متوجه شدید معنی واژه حداقل به معنی انتخاب بیشتر هستش - مطولب است حداکثر ۵ نفر انتخاب بشه
تو این وضعیت وقتی از واژه ” حداکثر ” استفاده میشه به این معنی هستش که مقادیر کمتر از ۵ نفر انتخاب بشن یعنی حالات مطلوب به این شکل در میاد : ۰ نفر ، ۱ نفر ، ۲ نفر ، ۳ نفر ، ۴ نفر و نهایت بیشترین مقدار ممکنه حداکثر ۵ نفر انتخاب شود.
درسنامه ششم
هدف درسنامه : زیر مجموعه های یک مجموعه
خلاصه درسنامه : درسنامه ششم اختصاص پیدا کرده به موضوع زیرمجموعه های یک مجموعه و تعداد نقاط انتخابی در یک دایره و …. که برای حل سوالاتی به این شکل ار فرمول ترتیب باید استفاده کرد.
- تعداد کل زیر مجموعه های یک مجموعه n عضوی از رابطه ۲n بدست می آید.
- تعداد زیر مجموعه های m عضوی از یک مجموعه n عضوی از رابطه (C(n,m بدست می آید.مثال : تعداد زیر مجموعه های ۴ عضوی یک مجموعه ۵ عضوی چقدر است؟
c( 5 , 4 ) = 5!/1! 4! = ۵
درسنامه هفتم
هدف درسنامه : جایگشت حروف به هم چسبیده
خلاصه درسنامه : تو درسنامه آخر در مورد جایگشت حروف به هم چسبیده صحبت کنیم ، بصورت مثال می خواهیم با کلمات ” مهربان ” کلمات ۶ حرفی بسازیم به نحوی که سه حرف ” م ، ه ، ر ” به هم چسبیده باشند. برای حل اینگونه سوالات کلماتی که به هم چسبیده شدند رو یک خونه در نظر میگیریم یعنی سه حرف ” م ، ه ، ر ” در کل میشن یه خونه و با سه حرف ” ب ، آ ، ن ” در مجموع میشه ۴ حرف و تا اینجا میشن !۴ و در ضمن خود سه حرف ” م ، ه ، ر ” هم !۳ حالت جایگشت خواهند داشت پس جواب نهایی میشه حاصل ضرب این حالت ها یعنی !۳ × !۴


سلام دوستانم فیلم ها رو براشون اشتراک گذاشتم خیلی از تدریستون راضی بودن دعا میکنم خدا یارو یاور و پشتیبانتون باشه
سلام من اولین بار از فیلم های ریاضی تدریس عالیتون دیدم بعد چند تا دیگه از آپارات ذخیره کردم خلاصه نزدیک 80تا فیلم از تدریس تون دیدم نتیجه امسالم خیلی خوب بود 20
خیلی عالی میشد اگه میتونستم بقیه تدریس ها رو هم ببینم از ریا ضی یازدهم چون دهم خوب ازتون یاد گرفتم .
سلام خیلی دوست دارم از تدریس های شیمی تون استفاده کنم خیلی سوالات عالی جواب میدید شیفته تدریستون شدم .
بعضی از دبیرا مطالب خیلی بزرگ میکنن اما شما کاملا میرید تو دل سوال واونو کاملا توضیح میدید ریز نکات اون رو هم میگید معلم چیره دست پایدار باشید وسایه شما بر سر ما مستدام باشد
سلام واقعا شیفته تدریس عالیتون هستم دوست دارم فیزیک رو ازتون یاد بگیرم .
سلام من ازتدریستون واقعا راضی ام واقعا از دل و جون مایه میذارید . مطالب پیچید نمی کنید ،.
سلام میگم روش تون خیلی درست خیلی از تدریستون خوشم میاد.
سلام خیلی دوست دارم شیمی ازتون یاد بگیرم .چون از هر نظر از تدریس شما تو زمان کوتا ه میشه چیز های زیادی فرا گرفت .
خیلی تو تدریس حرفه ای هستید کامل مطلب تو ذهن دانش آموزتون جا میندازند روش تدریسون عالی خارق العاده هستید