به غیر از زوایای معروف مثلثاتی مثل ۳۰ ، ۴۵ و ۶۰ درجه گاهی در برخی از سوالات فیزیکی لازم می شود که دانش آموزان زوایای دیگری مثل . پس اگر در اینترنت به دنبال روشی ساده برای حفظ کردن سینوس و کسینوس ۳۷ و ۵۳ درجه بودهاید، به مکان درستی آمدهاید. در این پست آموزشی قصد داریم روشی را آموزش دهیم که با یک تکنیک ساده مقادیر این زوایا رو بدرستی حفظ کنید. قبل از هر کاری به جدول زیر نگاه کنید تا با مقادیر این زوایا آشنا شوید.
| ۵۳ درجه | ۳۷ درجه | زاویه |
| ۰.۸ | ۰.۶ | Sin |
| ۰.۶ | ۰.۸ | Cos |
مطابق جدول بالا خواهیم داشت …..
Sin (۵۳) = ۰.۸
Cos (۵۳) = ۰.۶
Sin (۳۷) = ۰.۶
Cos (۳۷) = ۰.۸
مقادیر سینوس و کسینوس ۳۷ و ۵۳ درجه را چگونه حفظ کنیم؟
مطابق جدول بالا متوجه میشویم که مقدار سینوس و کسینوس ۳۷ و ۵۳ درجه ۰.۶ یا ۰.۸ میشود ولی مشکل در حفظ کردن این اعداد نیست مشکل در قاطی شدن این اعداد با هم شباهت زیاد این اعداد به هم است که باعث میشود این اعداد به جای هم نوشته شوند. بارها و بارها در کلاسهای تست زنی مشاهده کردهام که دانش آموزان این اعداد رو به جای هم استفاده میکنند و همین امر باعث میشود که جواب غلطی رو بدست بیاورند. حالا راه حل چیه؟
راه حل استفاده از دایره مثلثاتی و توجه به مقادیرِ ماکسیمم و مینیممِ سینوس و کسینوس هست.
یادآوری دایره مثلثاتی کسینوسها
مبحث دایره مثلثاتی در کتاب ریاضی دهم و یازدهم مطرح شده است و در دورههای مربوط به این قسمت این مباحث رو به صورت کامل آموزش دادهام، اما از میان همه نکاتی که در این دو فصل مطرح شده است تنها یک نکته برای حفظ صحیح مقادیر سینوس و کسینوس ۳۷ و ۵۳ درجه لازم است و اون نکته توجه دانش آموزان به مقادیر Max و Min سینوس و کسینوس درون دایره مثلثاتی است. خب پس وقت رو تلف نکنید و به تصویر زیر دقت کنید تا ضربه نهایی رو بزنیم و این اعداد شبیه به هم رو از پا در بیاریم…
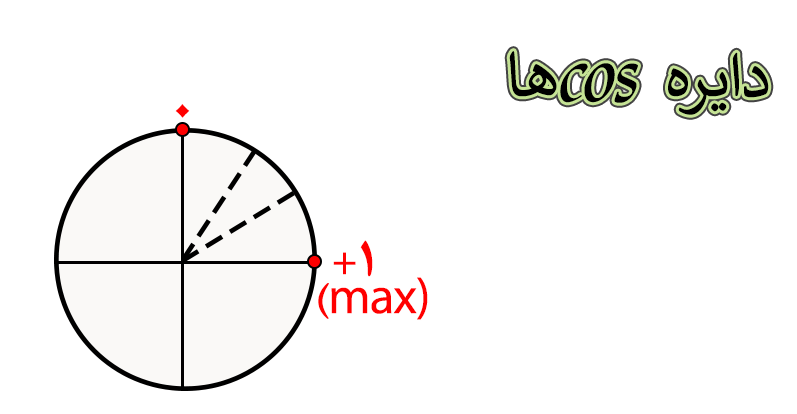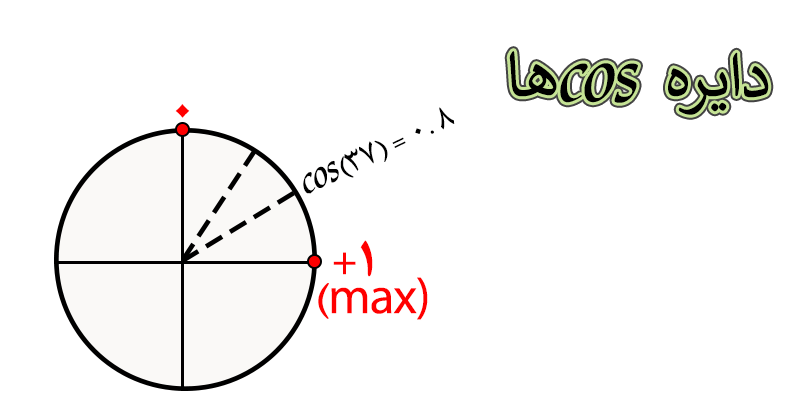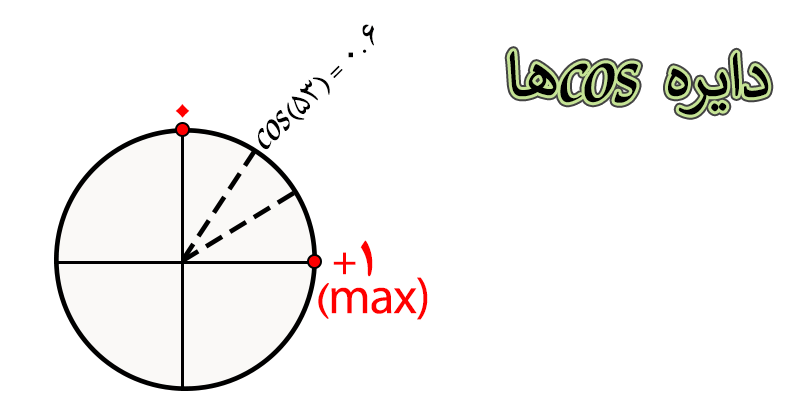
مطابق تصویر بالا متوجه میشویم که زاویه ۳۷ درجه در دایره مثلثاتی کسینوسها به مقدار Max یعنی عدد ۱+ نزدیکتر است، پس هنگام مقداردهی، اگر بین عدد ۰.۶ و ۰.۸ شک کردیم باید عدد بزرگتر یعنی عدد ۰.۸ رو انتخاب کنیم.
یعنی اگه بخوام کمی واضح تر توضیح بدم ، باید اینطوری بگم که Cos(37) یا برابر ۰.۶ میشه یا ۰.۸ که تو اینحالت کافی هستش دایره مثلثاتی کسینوس ها رو تجسم کنیم و بعد متوجه می شویم که زاویه ۳۷ درجه به مقدار max کسینوس ها نزدیکتر هستش ، پس cos(37) درجه باید ۰.۸ باشه نه ۰.۶
خب شاید بپرسین چرا اینجوریه ؟
به این علت که عدد ۰.۸ از عدد ۰.۶ بزرگتره پس باید به مقدار ماکسیمم نزدیکتر باشه.
یادآوری دایره مثلثاتی سینوسها
دقیقا مثل حالتی که برای کسینوس ها رسم کردیم اگر بخواهیم دایره مثلثاتی رو برای سینوس ها رسم کنیم متوجه می شویم که sin(53) به مقدار ماکسیمم یعنی به زاویه ۹۰ درجه نزدیک تر هست ، پس اگه بین دو عدد ۰.۶ یا ۰.۸ شک کردیم باید مقدار ۰.۸ رو به عنوان جواب sin(53) انتخاب کنیم.
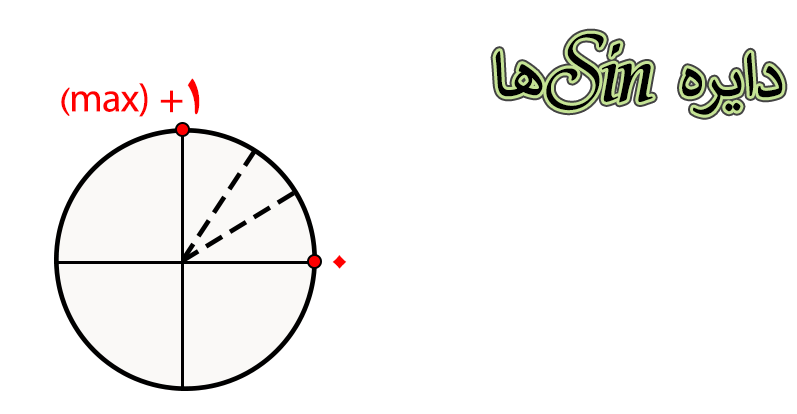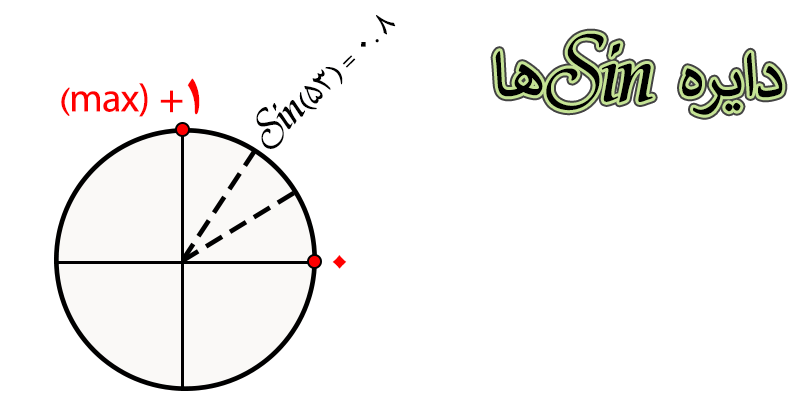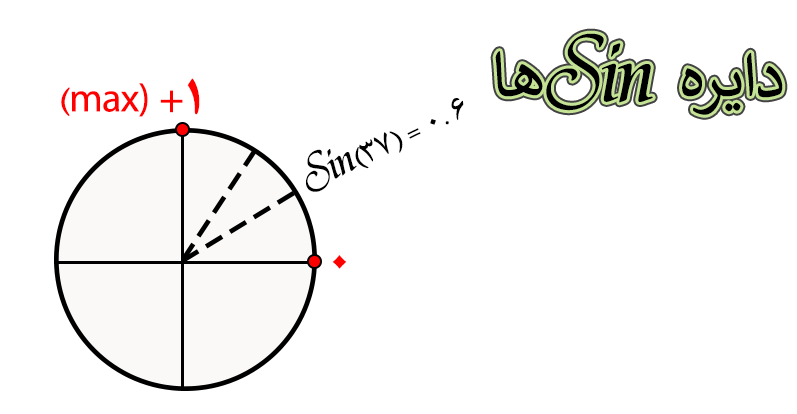
ضمنا اگر بخواهیم مقدار Sin(37) درجه رو انتخاب کنیم ، با توجه به اینکه سینوس ۳۷ درجه به مقدار زاویه صفر نزدیک تر هستش باید مقدار ۰.۶ رو به عنوان جواب انتخاب کنیم.
مقدار تانژانت و کتانژانت ۳۷ درجه چقدر است؟
مقدار تانژانت زاویههای ۳۷ درجه و ۵۳ درجه را به راحتی میتوان با تقسیم سینوس بر کسینوس محاسبه کرد. بصورت مثال فرض کنید که میخواهیم مقدار تانژانت ۳۷ درجه را محاسبه کنیم برای اینکار کافی است که سینوس ۳۷ درجه را تقسیم بر کسینوس ۳۷ درجه کنیم تا به راحتی به جواب مورد نظر برسیم.
مقدار کتانژانت ۳۷ درجه چقدر است؟
برای محاسبه مقدار کتانژانت ۳۷ درجه براحتی می توان از وارون تانژانت استفاده کرد یا اینکه به تعریف تابع کتانژانت رجوع کرد یعنی مثلا برای محاسبه مقدار کتانژانت ۳۷ درجه کسینوس زاویه ۳۷ درجه را بر سینوس زاویه ۳۷ درجه تقسیم کنیم ….
مثلث طلایی (مثلث ۳ و ۴ و ۵)
در قسمتهای قبلی با سینوس، کسینوس، تانژانت و کتانتانژت زاویه ۳۷ درجه و ۵۳ درجه آشنا شدید، در این قسمت باید یک نکته اضافهتری رو هم یاد بگیرید و اون نکته این هست که زاویههای ۳۷ درجه و ۵۳ درجه مربوط به مثلث قائم الزاویه با طول اضلاع ۳ و ۴ و همچنین وتر ۵ هست، در این مثلث زاویه ۳۷ درجه روبروی ضلع ۳ و زاویه ۵۳ درجه روبروی ضلع ۴ قرار داره، دونستن این نکته در بعضی از سوالات و تستهای فیزیک باعث افزایش سرعت محاسباتتون میشه. برای درک عمیقتر به تصویر زیر دقت کنید.
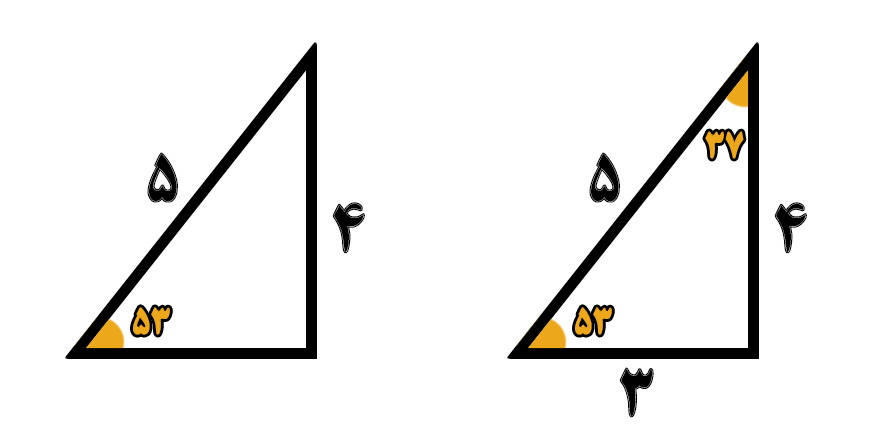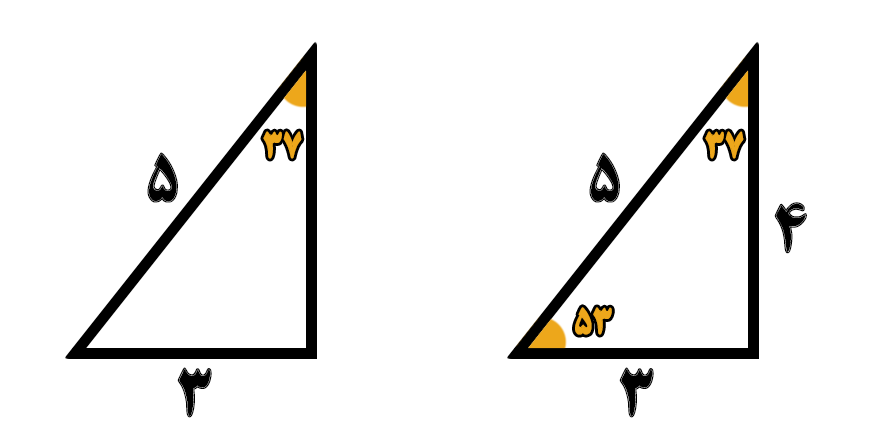
اگه به تصویر بالا دقت کنید مقابل زاویه ۵۳ درجه عدد ۴ و مقابل زاویه ۳۷ درجه عدد ۳ نوشته شده است. همانطوری که قبلا اشاره کردم در حل بعضی از سوالات و تستهای فیزیکی دونستن این نکته کمک زیادی به سادهتر شدن حل مساله میکنه…
فیلم آموزش زوایای ۳۷ درجه و ۵۳ درجه
برای تکمیل اطلاعات خودتون و یادگیری نکات بیشتر فیلم آموزشی این قسمت رو نگاه کنید و بعد از اون به سوال پایین ویدئو پاسخ بدین.
سوال : در یک مثلث قائم الزاویه که طول اضلاع آن ۳ و ۴ و ۵ است ، زاویه روبروی ضلع ۴ چقدر است؟
پاسخ هاتون رو زیر همین پست با ذکر دلیل کامنت کنید به اولین کامنت صحیح کد تخفیف ۵۰ درصدی از دوره های آموزشی لپ کلام ارائه می شود.
دقیقا خلاصه خلاصه و لپ کلام خیلی عالییی🎀
خیلی ممنونم خوشحالم که براتون مفید بوده
دمتونننن گرم استادددد واقعا در به در داشتم دنبال اینکه قضیش چیه میگشتم
سلام 53 درجه میباشد.
زاویه رو به روی ضلع ۴ زاویه ایست که sinاش برابر ضلع مقابل÷وتر = ۴/۵ یا همون ۰/۸ هست که مربوط به زاویه °۵۳ است
سلام ، ممنون بابت کامنت سبزتون ، بله پاسختون درست بود از تلگرام به شماره 09117636268 پیام بدین و کد تخفیفتون رو دریافت کنید.