تابع جز صحیح چه تابعی است ؟
تابع جز صحیح تابعی است که خروجی آن همیشه یک عدد صحیح است. یعنی فاقد جزء اعشاری می باشد. این تابع رو میتوان اینگونه هم تعریف کردکه با جزء اعشاری عدد ورودی قهر است. نام این تابع مهم نشان دهنده همین موضوع است. اگر ورودی این تابع یک عدد اعشاری مثلاً 2/3 به محض ورود به تابع جزء صحیح قسمت اعشارحذف می شود و خروجی تابع یک عدد صحیح یعنی عدد 2 می شود.
این تابع چگونه عمل می کند؟
به ازای ورودی های تابع دو حالت داریم.
حالت اول : وقتی ورودی تابع یک عدد صحیح باشد.
اگر ورودی تابع یا عددی که به تابع می دهیم صحیح باشد حال چه یک عدد منفی باشد و چه یک عدد مثبت باشد عینا خود عدد را بدون هیچ تغییری در خروجی تابع می بینیم.
[-2]= -2
[3]= 3
[0]= 0
[5]= 5
[-21]= -21
حالت دوم : وقتی ورودی تابع یک عدد غیرصحیح یا اعشاری باشد.
اگر ورودی تابع جزء صحیح یک عدد غیر صحیح یا اعشاری باشد یعنی با عددی روبرو باشیم که دارای قسمت اعشاری باشد حال چه یک عدد مثبت و چه عدد منفی باشد این عدد حتما بین دو عدد صحیح متوالی قرار دارد برای این حالت جزء صحیح عدد اعشاری برابر با عدد صحیح کوچکتر است. یعنی به صورت خلاصه می توان گفت که همیشه همیشه قسمت اعشاری عدد حذف شده و عدد به سمت پایین گرد می شود بصورت مثال جزء صحیح عدد 2.9 و عدد 2.8 و عدد 2.7 با این تعریف یکسان می شود یعنی قسمت اعشاری این اعداد حذف شده و عدد به سمت پایین گرد می شود. به مثال زیر دقت کنید.
[3.5]= 3
عدد 3.5 بین دو عدد صحیح متوالی 3 و 4 است پس با حذف قسمت اعشاری عدد به سمت پایین گرد ، و جواب نهایی 3 می شود.
به یک مثال دیگر دقت کنید
[-4.5] = -5
عدد 4.5- بین دو عدد صحیح متوالی -5 و -4 است یعنی 4->4.5->5- و از این دو عدد صحیح متوالی -5 کوچکتر است. در نتیجه خروجی تابع برابر -5 می شود.
برای تفهیم بهتر این مطلب، به جدول زیر دقت شود.
| [x] | عدد صحیح کوچکتر | دو عدد صحیح متوالی | عدد ورودی تابع یا x |
| 1 | 1 | 2>1.5>1 | 1.5 |
| 2- | 2- | 1->1.5->2- | 1.5- |
| 2 | 2 | 3>2.5>2 | 2.5 |
| 3- | 3- | 2->2.5->3- | 2.5- |
| 4 | 4 | 5>4.5>4 | 4.5 |
| 3 | 3 | 4>3.25>3 | 3.25 |
| 4- | 4- | 3->3.25->4- | 3.25- |
نکته 1: یک روش دیگر برای محاسبه ورودی های غیرصحیح منفی در تابع جزء صحیح این است که قسمت صحیح عدد منفی غیرصحیح را با -1 جمع بزنیم.
مثال :
[-1.5]= -1-1=-2
قسمت صحیح عدد -1/5 برابر -1 و قسمت اعشار آن -0/5 است پس قسمت صحیح که -1 است را با -1 جمع می زنیم که حاصل -2 است.
توضیح : به تابع جزء صحیح، تابع پله ای هم گفته می شود که این نامگذاری به دلیل شکل این تابع است.
تابع جزء صحیح چگونه رسم می شود؟
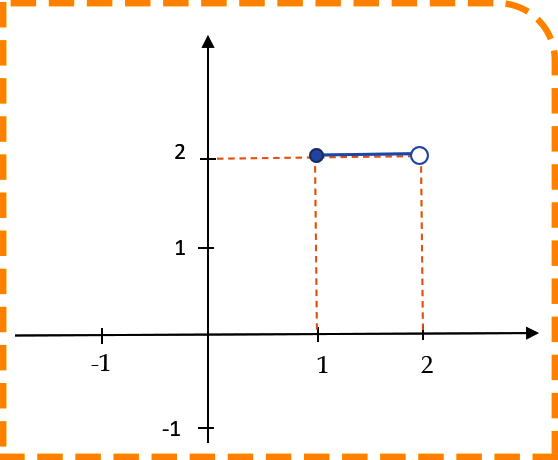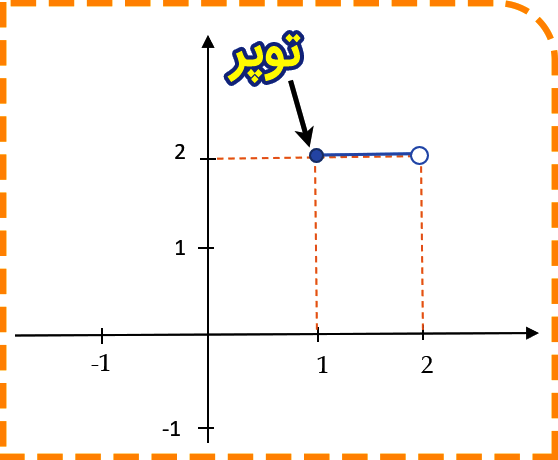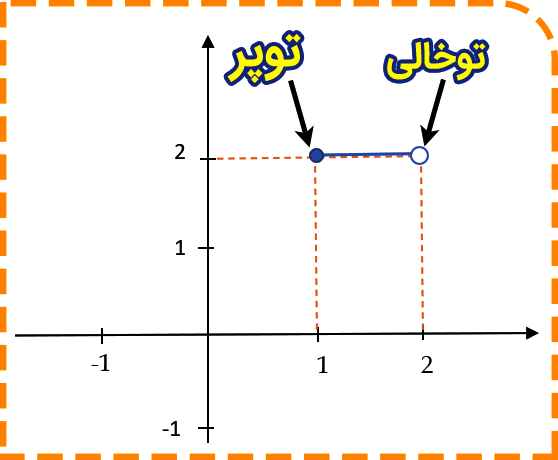
از آنجایی که تابع جزء صحیح اعداد را به سمت پایین گرد می کند از همین تکنیک برای رسم تابع جزء صحیح استفاده می شود . یعنی کافی است که ابتدا تابع اصلی بدون در نظر گرفتن جزء صحیح رسم شود و سپس y های رسم شده بین هر دو عدد صحیح شکسته شود. دقت شود که همیشه ابتدای هر بازه بسته ( توپر ) و انتهای آن باز ( توخالی ) خواهد بود زیرا همیشه تابع جز صحیح اعداد را به سمت پایین گرد می کند. به تصویر زیر دقت کنید تا درک بهتری نسبت به رسم توابع جزء صحیح داشته باشید.
اما رسم کامل نمودار جز صحیح چگونه است؟
رسم تابع جزء صحیح یا پله ای را در قالب یک مثال توضیح میدهیم؛
مثال: تابع y=[x] را در بازه (2,2-] رسم کنید.
گام نخست: به محض دیدن بازه در جزء صحیح آن را به بازه های کوچک با طول یک تبدیل می کنیم. زیرا رفتار تابع جزء صحیح در هر بازه به طول یک متفاوت است پس؛
[-2,2) → [-2,-1) , [-1,0) , [0.1) , [1.2)
دقت شود که این بازه ها متوالی و پشت سرهم هستند. پس به ازای اینکه x در چه بازه ای قرار بگیرد خروجی تابع جزء صحیح متفاوت است پس این بازه ها را بصورت زیر به ازای x می نویسیم؛
-2 ≤ x < -1
-1 ≤ x < 0
0 ≤ x < 1
1 ≤ x < 2
🔔 اما چرا دراین بازه ها سمت چپ همه دارای علامت مساوی هستند؟ چرا در سمت راست علاوه بر علامتر کوچکتر، علامت تساوی نداریم؟
زیرا تابع به ازای عدد ابتدای بازه و اعداد بین بازه یک جور رفتار می کند و به ازای عدد انتهای بازه یک جور دیگر. پس مجبوریم برای محاسبه جزء صحیح عدد انتهای بازه آن را در ابتدای بازه بعد با توجه به تقسیمات بازه ها قرار داده که جزء صحیح آن با اعداد میان بازه های بعد هم خوانی داشته باشد.
به بیان دیگر برای بازه 0 ≤ x < 1 جزء صحیح عدد صفر و اعداد بین صفر و 1 همه برابر صفر ولی جزء صحیح 1 برابر 1 است پس نمی توانیم برای علامت سمت راست مساوی قرار دهیم چون در محاسبه جزء صحیح دچار مشکل می شویم بنابراین جزء صحیح عدد صفر و اعداد بین صفر و 1 با جزء صحیح عدد 1 مساوی نیستند.
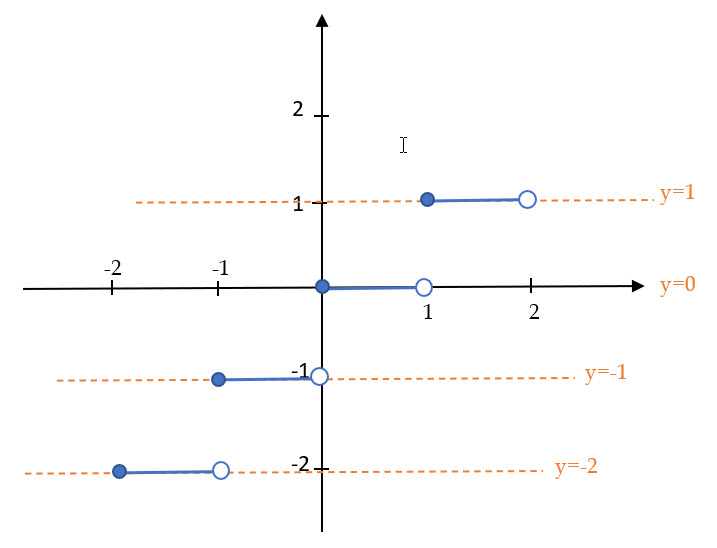
گام دوم: محاسبه جزء صحیح به ازای هر بازه است که برای این کار طبق توضیحات قبل فقط کافی است که عدد سمت چپ بازه یا عدد کوچکتر را قید کنید یعنی؛
-2≤x<-1 👉 [x]= -2 → y=-2
-1≤x<0 👉 [x]=-1 → y=-1
0≤x<1 👉 [x]=0 → y=0
1≤x<2 👉 [x]=1 → y=1
مثال1: حاصل [7.5-] + [3] را بدست آورید.
[-7.5]=-8
[3]=3
جز صحیح عدد 7.5- به سمت عقب گرد می شود پس برابر منفی هشت می شود و اما جز صحیح عدد 3 خود 3 می شود چرا؟ زیرا عدد 3 هیچ گونه ممیزی ندارد پس خود عدد 3 به عنوان خروجی از جز صحیح خارج می شود.
نکته :
⭐ جزء صحیح عدد اعشاری منفی برابر قسمت صحیح آن بعلاوه -1 می شود.
⭐ عدد صحیح خودش از جزء صحیح بیرون می آید
[7.5-] + [3] = -8 + 3 = -5
مثال2: حاصل [1.5-]-[2.25-]2 را بدست آورید.
[-1.5]=-1-1=-2
یا
-2<-1.5<-1 👉 [-1.5]=-2
[-2.25]=-2-1=-3
یا
-3<-2.25<-2 👉 [-2.25]=-3
جزء صحیح عدد اعشاری منفی می شود و قسمت صحیح آن بعلاوه -1 می گردد.
یا عدد اعشاری را با توجه به محور مختصات بین دو عدد متوالی قرار داده و عدد صحیح کوچکتر، جواب است. دقت کنید که ضریب پشت جزء صحیح به هیچ وقت حق ندارد به درون جزء صحیح برود ، یعنی در سوال بالا عدد 2 رو حق نداریم در عدد 2.25- ضرب کنیم و بعد از ساده سازی به جواب نهایی برسیم ، همیشه همیشه همیشه اول از همه عبارت داخل جز صحیح رو باید ساده کنیم و بدست بیاریم بعدا در ضریب پشت خودش ضرب کنیم ، با این اوصاف خواهیم داشت ….
2×[-2.25]-[-1.5] = 2 × (-3) – ( -2 ) = -6 + 2 = -4
مثال3: حاصل [3.5-]+[3.5] را بدست آورید.
[3.5]=3
یا
3<3.5<4 👉 [3.5]=3
[-3.5]=-3-1=-4
یا
-4<-3.5<-3 👉 [-3.5]=-4
جزء صحیح عدد اعشاری مثبت برابر با قسمت صحیح عدد یا اینکه روی محور نگاه می کنیم که این عدد بین چه اعداد صحیح متوالی قرار گرفته و عدد کوچکتر، جواب است ، پس خواهیم داشت ….
[3.5]+[-3.5] = 3 + (-4) = -1
مثال قبلی رو میشه با نکته هم حل کرد ، چه نکته ای ؟ به تصویر زیر دقت کنید.
طبق این نکته اگر x عددی صحیح باشه ( یعنی بدون اینکه حساب کتاب خاصی انجام بدیم می دونیم که جواب آخر میشه 0 و اگه x عددی اعشاری باشه جواب نهایی همیشه 1- میشه .
که حالت x∉z در مثال قبل مشاهده شد پس جواب نهایی 1- می شود.
مثال4: مقدار [ 1-[x] ] به ازای x=-1/2
گام اول: عدد 1/2- رو در تابع جایگذاری می کنیم پس داریم؛
گام دوم: [1/2-] که جزء صحیح داخلی است را محاسبه می کنیم؛
[-1/2]=[-0/5] 👉 [-0/5]=0-1=-1
or
-1<-0/5<0 👉 [-0/5]=-1
در اینجا عدد کسری داخل جزء صحیح را به صورت اعشاری نوشتیم و بعد جزء صحیح آن را محاسبه کردیم.
گام سوم: محاسبه جزء صحیح بیرونی بعد از جایگذاری گام دوم
مثال 5: حاصل [[5x]-[7x]] را به ازای x=-1/2 بدست آورید.
گام اول: جایگذاری x=-1/2 در تابع جزء صحیح؛
گام دوم: محاسبه جزء صحیح های داخلی؛
[-7/2]=[-3/5]=-3-1=-4 or -4<-3/5<-3 👉 [-3/5]=-4
[-5/2]=[-2/5]=-2-1=-3 or -3<-2/5<-2 👉 [-2/5]=-3
در اینجا اعداد کسری داخل جزء صحیح رو بصورت اعشاری نوشتیم و بعد جزء صحیح رو محاسبه کردیم.
گام سوم: جایگذاری گام دوم و محاسبه حاصل تابع جزء صحیح
در این مرحله عدد داخل جزء صحیح، یک عدد صحیح می شود.
[[7×-1/2]-[5×-1/2]]=[-4-(-3)]=[-4+3]=[-1]=-1
تابع y=x-[x]
دامنه این تابع R است
برد این تابع بین 0 و 1 است
x ∈ R
0≤x-[x]<1
Df=R
Rf=[0,1)
رسم تابع y=x-[x]
با توجه به دامنه و برد این تابع، اگر بخواهیم تابع را روی بازه (2,2-] رسم کنیم خواهیم داشت :
مرحله اول: تقسیم بازه اولیه به بازه های کوچک یک واحدی
-2 ≤ x < -1
-1 ≤ x < 0
0 ≤ x < 1
1 ≤ x < 2
مرحله دوم: محاسبه مقدار تابع به ازای هر بازه
تابع y = [x]+[-x]
اگر بخواهیم این تابع را در بازه (2,2-] رسم کنیم؛
مرحله اول: بازه را به بازه های کوچک به اندازه یک واحد تقسیم می کنیم؛
-2 ≤ x < -1
-1 ≤ x < 0
0 ≤ x < 1
1 ≤ x < 2
مرحله دوم: به ازای هر بازه مقدار y را محاسبه می کنیم
-2≤x<-1 👉 x∉z y=-1 👉 x∈z y=0
-1≤x<0 👉 x∉z y=-1 👉 x∈z y=0
0≤x<1 👉 x∉z y=-1 👉 x∈z y=0
1≤x<2 👉 x∉z y=-1 👉 x∈z y=0


یه سوال داشتم ۰.۷ براکتش چند میشه ۱-
سلام درخصوص حل معادلات براکتی توضیحی ندارین
سوالم این بود اگر داخل کوروشه ایکس دارای ضریب باشع چجوری جز صحیح رو به دست میاریم چون ضریب رو که نمیتونیم بیاریم بیرون مثلا [2x]
برای اینکار کافی هست ابتدا عدد مورد نظر رو ضرب کنید و بعدا با توجه به عدد مورد نظر مقدارش رو بدست بیارین یا اگه کلا بر حسب متغیر باشه بسته به مدل سوال روشهای مختلفی رو میشه پیشنهاد کرد
عالی بود واقعا
یه سوال داشتم اگه مثلا عبارتی به صورت [‘3-]-3باشه اون منفی پشت جزصحیح قبلش تو جزصحیح ضرب میشه ؟
*اون علامت (‘) همون منفی بالای ۳هست یعنی چپ ۳
خود عبارتم اینه[x-]-x که x به چپ ۳ میل می کند
سلام دوست خوبم ، نه اون منفی پشت جزء صحیح نمیتونه داخلش ضرب بشه
خیلی عالی و کامل
من خیلی ممنونم بابت زحماتتون
writermojin@gmail.com