برای دسترسی کامل به دوره، خریداری کنید
دوره آموزشی مثلثات ( فصل چهارم ریاضی یازدهم تجربی )
فصل چهارم ریاضی یازدهم تجربی در مورد مبحث مثلثات است ، در فصل چهارم ریاضی یازدهم تجربی با مفهوم رادیان و درجه و تبدیل این دو زاویه مثلثاتی به هم ، زوایایی مثل ۵π/۶ ، ۴π/۳ و زوایایی مثل ۲۴۰ درجه و همچنین رسم توابع مثلثاتی آشنا می شوید. ضمنا در این فصل مفاهیم دایره مثلثاتی تکمیل تر می شود…
معرفی زاویه رادیان و درجه
در فصل مثلثات ریاضی یازدهم تجربی با دو مدل زاویه بررسی قرار میگیره
زاوبه بر حسب درجه مثل ۳۰ درجه و ۴۵ درجه که تو دهم باهاش آشنا شدین
حالت بعدی زاویه بر حسبت رادیان هست که تو کتاب یازدهم باهاش آشنا میشین و یاد میگیرین که چطور این دو زاویه رو به هم تبدیل کنید.
اندازه یک زاویه بر حسب رادیان یعنی طول کمان روبروی زاویه تقسیم بر شعاع دایره ، واحد رادیان بر حسب π نوشته می شود و هر π رادیان معادل ۱۸۰o درجه است. در مجموع روابط زیر رو میشه بین رادیان و درجه نوشت…
روابط تکمیلی بین نسبت های مثلثاتی
در سال گذشته با زوایای ۰ ، ۳۰ ، ۴۵ ، ۶۰ ، ۹۰ ، ۱۸۰ ، ۲۷۰ و ۳۶۰ درجه آشنا شدید ، در کتاب ریاضی یازدهم زوایای مثلثاتی تکمیل تر شده و بصورت مثال با زوایای منفی هم آشنا می شوید ، یعنی یاد میگیرید که بصورت مثال cos(-30) چطور محاسبه میشه و یا اینکه با زاویه Cos(90-∝ ) به چه شکل محاسبه می شود…
فرمول زوایای منفی نسبت های مثلثاتی :
Cot(-∝) = –Cot(∝)
tan(-∝) = –tan(∝)
Sin(-∝) = –Sin(∝)
Cos(-∝) = Cos(∝)
اگه به روابط بالا دقت کنید زوایای منفی هر نسبت مثلثاتی به غیر از Cosها قرینه حالت مثبت خودش میشه ، یعنی به یک بیان ساده میشه گفت که منفی رو میشه از داخل کمان Sin tan و Cot بیرون کشید ولی منفی در Cosها جذب می شود … به مثال های زیر دقت کنید…
Cot(-60) = – √۳/۳
tan(-60) = – √۳
Sin(-60) = – √۳/۲
Cos(-60) = 1/2
فرمول نسبت های مثلثاتی زوایای مکمل :
منظور از زوایای مکمل فرمول هایی مثل Cos(π–∝ ) و Sin(π–∝ ) و tan(π–∝ ) و … است. کلیه روابط مربوط به این قسمت درون تصویر زیر می توانید ببینید…
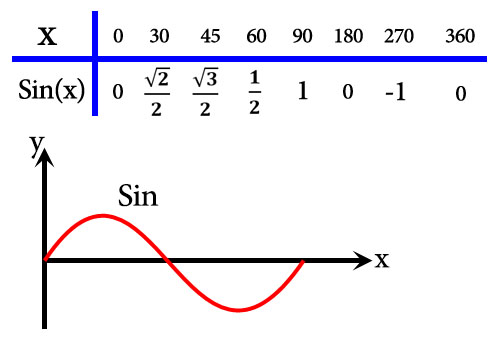
رسم توابع مثلثاتی
بخش آخر این فصل در مورد رسم توابع مثلثاتی صبحت شده است که از میان ۴ تابع سینوس ، کسینوس ، تانژانت و کتانژانت فقط رسم تابع سینوس و کسینوس بحث شده است. برای رسم توابع مثلثاتی در این فصل از روش نقطه گذاری و انتقال تابع استفاده می شود ، روش نقطه گذاری به این صورت هست که به تابع مثلا سینوس مقادیر مختلفی داده می شود و نقطه مورد نظر در صفحه مختصات رسم می شود و سر آخر با اتصال این نقاط به هم تابع مثلثاتی رسم می شود . برای درک بهتر توابع سینوسی و کسینوسی به تصویر این قسمت دقت کنید.
