برای دسترسی کامل به دوره، خریداری کنید
آموزش ریاضی دهم – فصل پنجم ( تابع )
دوست خوبم سلام ،
به دوره آموزشی ریاضی دهم فصل پنجم خوش اومدین. فصل پنجم ریاضی نهم در مورد مفهوم تابع هستش ، در این دوره آموزشی با مفهوم تابع خطی ، تابع یک به یک ، نمایش تابع به عنوان زوج مرتب ، تشخیص تابع از روی نمودار ، تشخیص تابع از روی ضابطه و … آشنا می شین. ضمنا در این دوره کلیه مثال ها و تمرینات کتاب درسی ریاضی نهم درسی بصورت کامل در قالب ۹ درسنامه براتون حل کردیم ضمن اینکه در انتهای هر درسنامه تمریناتی مشابه همون درس تحت عنوان ” تمرین در منزل ” برای تمرین و تکرار بیشتر وجود داره . برای مشاهده درسنامه های رایگان فصل پنچم ریاضی دهم به پایین همین صفحه مراجعه کنید.
مفاهیم اولیه تابع
- آنچه خواهید آموخت : نمایش تابع به عنوان زوج مرتب ، بررسی تابع بودن یا نبودن در قالب نمودار ، بررسی شرایط تابع بودن یا نبودن
- زمان درسنامه : 28 دقیقه
- تعداد سوالات حل شده : 13 سوال
همونطوری که از اسم این مبحث مشخصه قراره که در مورد تابع اطلاعاتی کسب کنیم و تابع رو بررسی کنیم. تابع رو میشه از دیدگاه های مختلفی بررسی کرد که به ترتیب در مورد هر کدومش مختصرا توضیحاتی میدم
- نمایش تابع در قالب زوج مرتب
توی این حالت به زوج مرتبی تابع گفته میشه که یک به چند نباشه ، یعنی به ازای هر x فقط و فقط یک y وجود داشته باشه.
نکته : اگر درون زوج مرتبی دو یا چند y متفاوت وجود داشته باشه برای اینکه زوج مرتب تابع محسوب بشه باید x های برابر داشته باشن - نمایش تابع در قالب رسم نمودار
چنانچه یک منحنی در صفحه مختصات کشیده شده باشد در صورتی منحنی رسم شده تابع محسوب می شود که هر خط دلخواه موازی محور yها منحنی نمایش تابع را حداکثر در یک نقطه قطع کند ، بصورت خلاصه تر یعنی اگر در محور مختصات با رسم یک خط موازی محور yها ، منحنی در دو یا چند نقطه قطع شود در اینصورت منحنی رسم شده تابع محسوب نمی شود. - نمایش تابع در قالب عبارت های جبری
توضیح این قسمت کمی پیچیده هستش و شما دانش آموز عزیز رو ارجاع میدم به ویدئوهای آموزشی
مطالب بالا معرفی و آشنایی اولیه و سطحی با مفهوم تابع هستش بمرور در طی سال های مختلف توابع گوناگونی ( لگاریتمی ، نمایی ، چند جمله ای ، پیوسته و … ) معرفی خواهد شد.
تابع بودن یا نبودن مساله این است!
- آنچه خواهید آموخت : بررسی تابع بودن یا نبودن یک زوج مرتب با بررسی مولفه های x , y
- زمان درسنامه : ۱۹ دقیقه
- تعداد سوالات حل شده : ۶ سوال
هدف از این درسنامه بررسی تخصصی تر نمایش زوج مرتب ها به صورت تابع هستش. اول از همه بگم که منظور از نمایش زوج مرتب همون مولفه های x و y بصورت ( x , y ) هستش بصورت مثال مجموعه A یک زوج مرتب محسوب می شود.
A = { ( 1 , 3 ) , ( 5 , 7 ) , ( 1 , 3 ) , ( 9 , -2 ) }
هر زوج مرتبی تابع نیستش برای اینکه زوج مرتب ها تابع محسوب بشن بایستی شرایط زیر رو داشته باشن
- ایکس های متفاوتی داشته باشن
- اگر ایکس مشترکی دارن حتما حتما y مشترکی داشته باشن
یعنی بصورت خلاصه اگر یک زوج مرتب به ازای یک x مشترک دو یا چند y متفاوت داشته باشه تابع محسوب نمیشه.
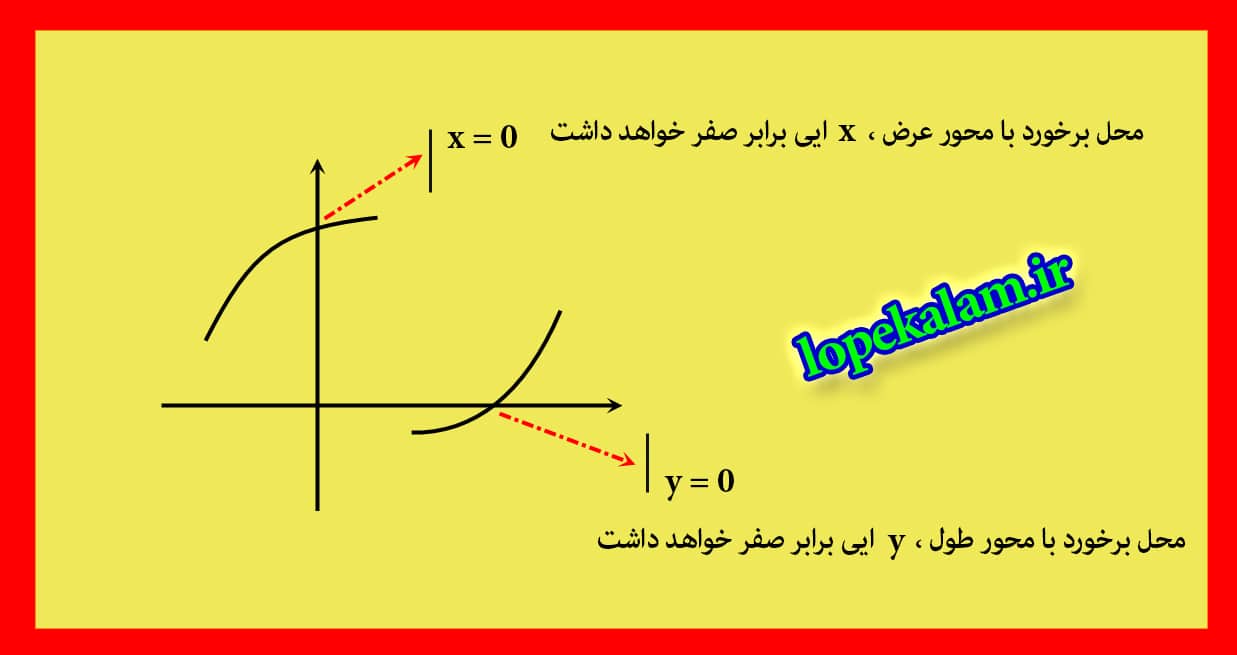
دامنه و برد یک تابع
- آنچه خواهید آموخت : بررسی دامنه و برد یک تابع از روی رسم نمودار ، پیدا کردن دامنه و برد تابع از روی نمایش زوج مرتب تابع
- زمان درسنامه : 28 دقیقه
- تعداد سوالات حل شده : 10 سوال
تو این درسنامه قراره بصورت مقدماتی با مفهوم دامنه و برد یک تابع آشنا بشین ، دامنه یک تابع یعنی اعدادی که مولفه ایکس یک تابع میتونه قبول کنه و بپذیره ، و بیشترین مقدار x ایی که یک تابع میتونه قبول کنه مجموعه اعداد حقیقی R هستش.
اما برد یک تابع مجموعه مقادیر y تابع هستش که توی این درسنامه بصورت خیلی مقدماتی در مورد ضابطه تابع هم صحبت میشه و مسائلی رو تحلیل و بررسی میکنیم.
مقدار دهی تابع
- آنچه خواهید آموخت : آشنایی با مفهوم مقدار دهی توابع y=f(x) و y=f(f(x))
- زمان درسنامه : ۳۰ دقیقه
- تعداد سوالات حل شده : ۱۰ سوال
وی این درسنامه در مورد مقدار دهی توابع بر حسب ضابطه هاشون باهاتون صحبت میکنم ، به مثال زیر دقت کنین.
مثال : تابع با ضابطه f(x) = x۳ + ۱ را در نظر گرفته و مقادیر ( (f(0) , f(1) , f(-2) , f( f(2 را بدست آورید.
راه حل
f(x) = x۳ + ۱
f(0) = 0۳ + ۱ = 1
f(1) = 1۳ + ۱ = 2
f(-2) = (-2)۳ + ۱ = -۸+۱ = -۷
f( f(2) ) = f ( 2۳ + ۱ ) = f ( 8 + 1 ) = f(9) = 9۳ + ۱ =۷۳۰
تابع خطی
- آنچه خواهید آموخت : آشنایی با تابع خطی f(x) = a x + b ، محاسبه دامنه و برد تابع خطی و مقداردهی تابع خطی
- زمان درسنامه : 29 دقیقه
- تعداد سوالات حل شده : 7 سوال
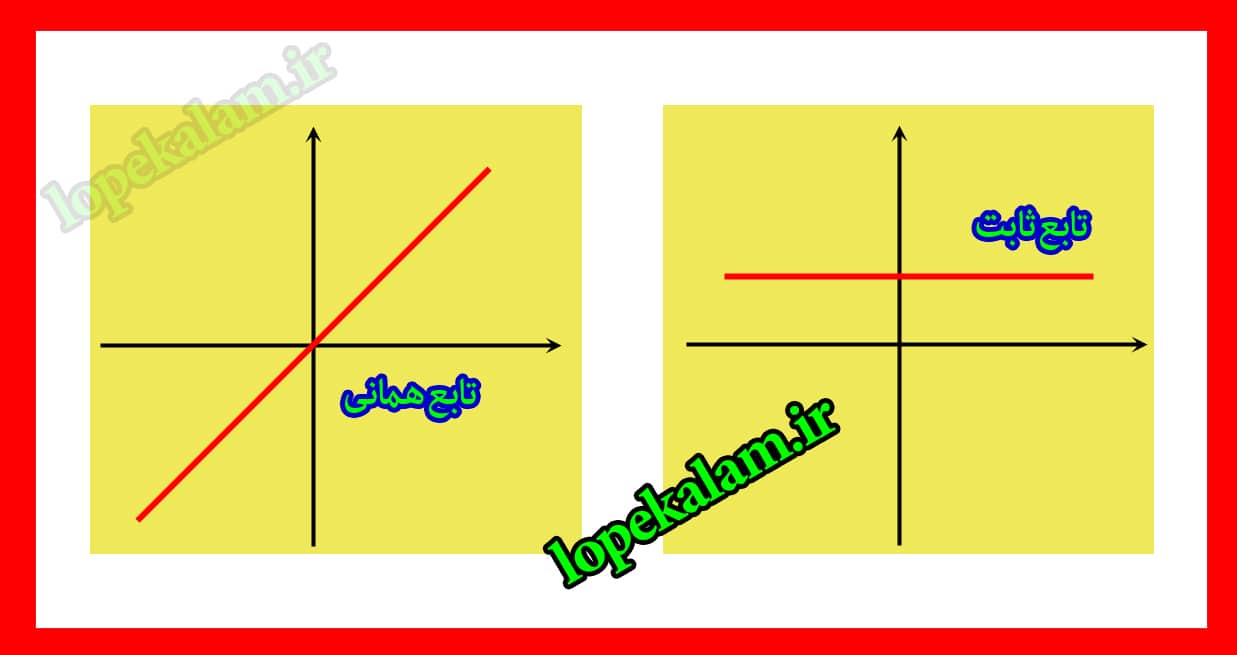
تابع همانی و تابع ثابت
- آنچه خواهید آموخت : آشنایی با تابع ثابت و تابع همانی ( y = x , y = a , x = a )
- زمان درسنامه : 32 دقیقه
- تعداد سوالات حل شده : 12 سوال
مثال های بیشتر از تابع همانی و تابع ثابت درون درسنامه ششم بحث و بررسی میشه. تابع همانی در واقع تابع y = x هستش یعنی x , y برابر هستن
توابع چند ضابطه ای(قطعه ای)
- آنچه خواهید آموخت : آشنایی اولیه با توابع چند ضابطه ای ، مقدار دهی توابع چند ضابطه ای ، رسم توابع چند ضابطه ای
- زمان درسنامه : 22 دقیقه
- تعداد سوالات حل شده : 12 سوال
یکی از مفاهیم مهم این فصل تابع چند ضابطه ای یا قطعه ای هستش ، در واقع داستان از این قراره که بعضی از توابع بر حسب دامنه و ضابطه هاشون به چند قطعه مختلف تقسیم میشن ، به اینگونه از توابع ، توابع چند ظابطه ای گفته میشه. راستی تا یادم نرفته اسم دیگه تابع چند ظابطه ای تابع قطعه ای هم هست. مهمترین نکته ای که در مورد توابع قطعه ای باید یاد بگیرین این نکته هستش که تحت چه دامنه ای x رو داخل تابع قرار بدین و موقع جاگذاری عددی ضابطه درست رو تشخیص بدین. به تصویر زیر دقت کنین تا با تابع چند ضابطه ای بیشتر اشنا بشین.

تابع چند ضابطه ای پیشرفته ( قطعه ای )
- آنچه خواهید آموخت : آشنایی با مقدار دهی توابع چند ضابطه ای ، رسم توابع چند ضابطه ای و قطعه ای ، محاسبه دامنه و برد توابع چند ضابطه ای
- زمان درسنامه : 40 دقیقه
- تعداد سوالات حل شده : 12 سوال
توی درسنامه قبلی بیشتر در مورد مقداردهی توابع چند ضابطه ای صحبت کردیم ولی توی درسنامه هشتم میخوایم در مورد رسم توابع چند ضابطه ای صحبت کنیم . تنها نکته ای که در مورد رسم توابع چند ضابطه ای باید بدونین این هستش که هر تابع رو با توجه به دامنه خودش رسم کنید و ضمنا توجه کنید که تابع شما خطی ، ثابت و یا سهمی شکل هستش به تصویر زیر دقت کند و یک نمونه رسم تابع چند ضابطه ای رو مشاهده کنید.

رسم توابع به کمک انتقال
- آنچه خواهید آموخت : رسم توابع قدرمطلقی به کمک مفاهیم انتقال تابع ، رسم توابع سهمی شکل به کمک انتقال تابع
- زمان درسنامه : 30 دقیقه
- تعداد سوالات حل شده : 13 سوال
رسم توابع به کمک انتقال آخرین موضوع فصل تابع هستش که در سال های بعدی هم تکرار میشه ، اول از همه باید رسم یک تابع بصورت ساده رو بلد باشین تا بعدش بتونین از تکنیک انتقال برای رسم استفاده کنین.
توی درسنامه نهم ۲ مدل رسم به کمک انتقال رو بررسی میکنیم.
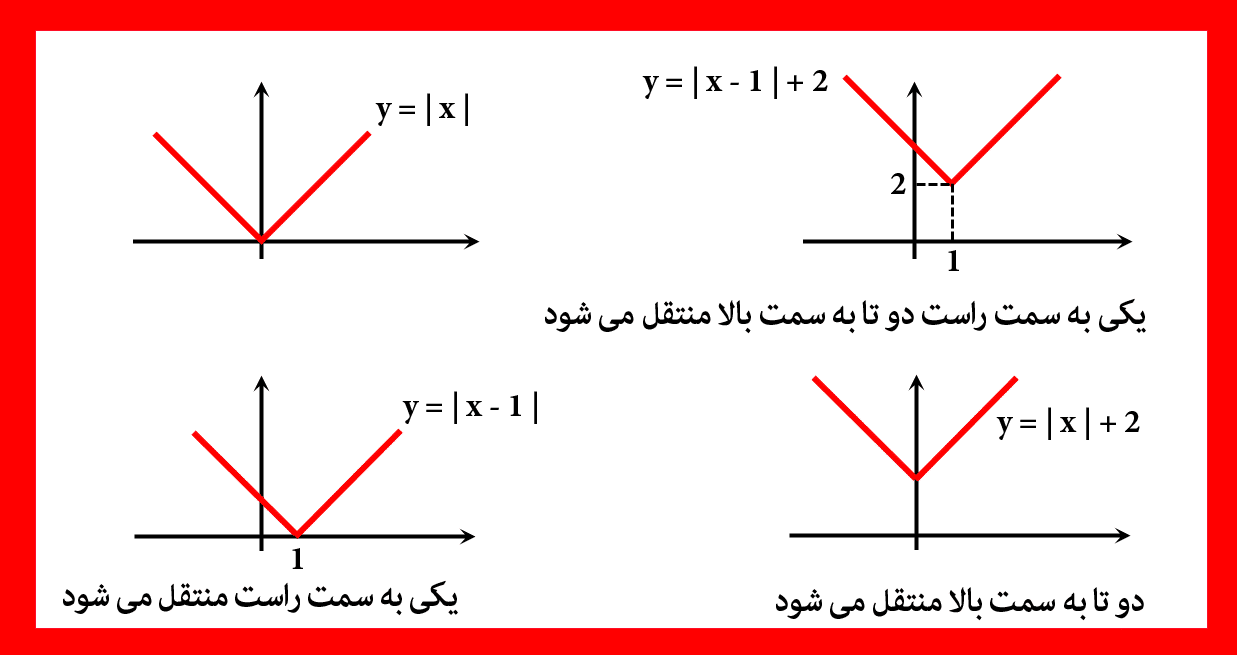
- رسم تابع قدرمطلقی | y = | x
تابع قدرمطلق به شکل هفت v هستش و کافیه که راس اون رو به نواحی مختلف انتقال بدیم.
برای مثال تابع | ۲ – y = | x دو واحد به سمت راست منتقل میشه یعنی برعکس اون چیزی که دیده میشه ( در واقع به اندازه ریشه داخل قدر مطلق تابع در جهت محور ایکس به سمت عقب و جلو منتقل میشه )مثال دوم :تابع ۳ + | y = | x به اندازه سه واحد به سمت بالا منتقل میشه یعنی اگه بعد از علامت قدرمطلق عددی اومد به همون اندازه در راستای محور yها تابع به سمت بالا و یا پایین انتقال پیدا میکنه ولی اگه عدد داخل قدرمطلق بودش به این معنی هستش که باید قدرمطلق رو به اندازه ریشه داخل قدر مطلق به سمت عقب یا جلو در راستای محور ایکس جابجا کرد.درضمن اگه پشت قدرمطلق ضریب داشته باشیم و ضریب منفی باشه باعث میشه قدرمطلق بجای اینکه هفت v رو به بالا باشه هفت رو پایین رسم میشه و اگه ضریب پشت قدرمطلق مثبت باشه که بصورت عادی قدرمطلق به سمت بالا رسم میشه. - رسم تابع سهمی y = x۲
مشابه مطالبی که برای تابع قدر مطلق گفته شد برای سهمی ها هم میشه همون مطالب رو گفتش و منطق انتقال توابع برای هر نوع تابعی یکسان هستش یعنی انتقال تابع سهمی ، قدرمطلقی ، رادیکالی و …. همه به یک شکل انجام میشه ، برای درک بهتر به مثال زیر دقت کنید.
اول از همه اینو بگم که تابع سهمی شبیه قدرمطلق هستش منتها گرد به سمت بالا رسم میشه تقریبا شبیه u منتها کمی پهن ترخوب بریم سراغ مثال هاشفرض کنید که میخوایم تابع y = ( x-3 )۲ رو به کمک انتقال رسم کنیم. برای رسم این تابع کافیه که سهمی رو ۳ واحد به سمت راست منتقل کنیم. حالا فرض کنید که میخوایم سهمی y = ( x+5 )۲ رو به کمک انتقال رسم کنیم توی این حالت کافیه که سهمی رو ۵ واحد به سمت چپ منتقل کنیم در واقع توی این جالت ریشه داخل سهمی یعنی راس سهمی ۵- = x هستش بخاطر همین سهمی ۵ تا به سمت چپ منتقل میشه. اما حالا فرض کنین که بخوایم سهمی ۴ + y = x۲ رو رسم کنیم توی این حالت که عدد ۴ خارج توان دو هستش دقیقا ۴ واحد به سمت بالا در راستای محور y منتقل میشه یعنی مشابه قدرمطلق اگه عددی خارج سهمی باشه به همون شکل به بالا و پایین منتقل میشه.