برای دسترسی کامل به دوره، خریداری کنید
دوره آموزشی هندسه تحلیلی و جبر (فصل اول ریاضی یازدهم)
فصل اول ریاضی یازدهم تجربی در مورد مباحثی مثل تابع خطی ، تابع درجه دوم ، مبحث مجموع و مضرب ریشه های معادله درجه دوم ، ماکسیمم و مینیمم سهمی ، حل معادلات گویا و رادیکالی و .. است که تمامی این موارد در این دوره آموزشی تدریس کردیم ، برای دسترسی به مباحث بر روی سر فصل های هر قسمت کلیک کنید.
- هندسه تحلیلی
- معادله درجه دوم و تابع درجه دوم ( مبحث S , P )
- معادلات گویا و معادلات رادیکالی
۱ . هندسه تحلیلی
ابتدای کتاب ریاضی یازدهم تجربی فرمول تابع خطی یادآوری می شود که در حقیقت این موضوع در ادامه فصل ششم ریاضی نهم است ، فرمول تابع خطی رو میشه به فرم های زیر نوشت.
f(x)= ax + b
در رابطه بالا منظور از a شیب خط و منظور از b عرض از مبدا خط است.
y = ax + b
در رابطه بالا منظور از a شیب خط و منظور از b عرض از مبدا خط است.
y – y۰ = m( x – x۰ )
در رابطه بالا منظور از m شیب خط است.
فرمول فاصله بین دو نقطه :
نکته بعدی که بسیار تو این فصل مهم هست فرمول فاصله بین دو نقطه هست که سهم ویژه ای در تست های کنکور داره و میتونه براحتی با موضوعات مختلف کتاب درسی ترکیب بشه …

شیب خط های موازی و عمود برهم :
اگه دو خط باهم موازی باشه در این صورت شیب دو خط با هم برابر خواهد بود ولی اگه دو خط بر هم عمود باشه در این صورت شیب دو خط عمود و قرینه خواهد بود.

فرمول فاصله نقطه از خط :
فرمول فاصله نقطه (x۰,y۰) از خط ax+by=0 برابر است با:
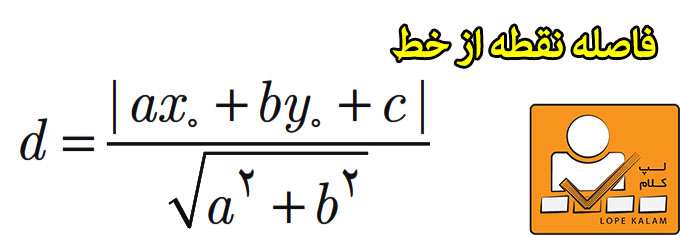
معادله درجه دوم و تابع درجه دوم ( مبحث S , P )
حل معادلات رادیکال و تغییر متغیر :
گاهی برای حل معادلات با درجه چهارم نیاز هست که معادلات رو به توان های کمتر ساده کنیم و بعد از اون شروع به حل مساله کنیم به این روش تغییر متغیر گفته می شود. ضمنا برا ی حل معادلاتی که درون اونها رادیکال وجود داره نیاز هست که طرفین معادله رو به توان ۲ برسونیم به تصویر روبرو دقت کنید…
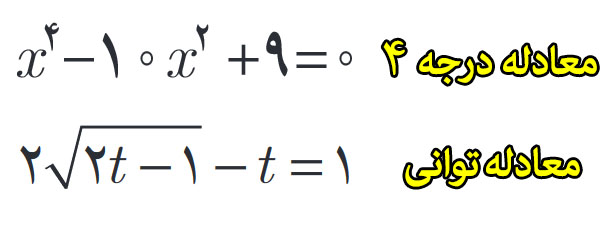
مجموع و حاصل ضرب ریشه های معادلۀ درجه ۲
یکی از مباحث بسیار بسیار مهم این فصل بحث مجموع و خاصل ضرب ریشه های معادله درجه دوم است که با فرمول های S و P شناخته می شوند . خلاصه این فرمول ها به این شکل که هرگاه مجموع ریشه های یک معادله درجه دوم y = ax۲ + bx + c رو حساب کنیم حاصل جمع ریشه ها همیشه میشه b/a- و حاصل ضرب ریشه ها میشه c/a ، البته باید دقت کنید که دلتای معادله درجه دوم منفی نباشه وگرنه در کل معادله فاقد ریشه میشه….

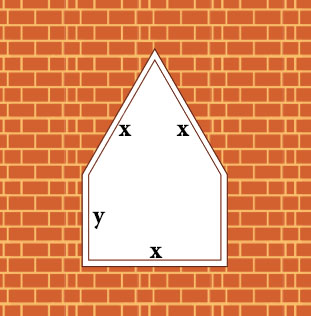
ماکزیمم و می نیمم سهمی
هدف این بخش کتاب درسی پیدا کردن مساحت بیشینه برای اشکال هندسی با تشکیل معادلات درجه دوم هست . بصورت مثال : یک پنجره به شکل مستطیلی است که در بالای آن یک مثلث متساوی الاضلاع قرار گرفته است. اگر محیط پنجره 4m باشد ، ابعاد مستطیل را طوری بیابید که پنجره حداکثر نوردهی را داشته باشد.
حل معادلات گویا :
به معادلاتی که در آنها مجهول در صورت و مخرج کسرها قرار داشته باشه معادله گویا می گویند ، برای حل معادلات گویا طرفین معادله رو در ( ب م م ) مخرج ها ضرب می کنند تا معادله از حالت کسری در بیاد فقط باید حواسمون جمع باشه که جواب های بدست اومده با دامنه اولیه توابع مشکلی نداشته باشه یعنی اینکه جواب بدست اومده جزو ریشه مخرج نباشه به تصویر و معادله نمونه دقت کنید.
