دسترسی کامل به این دوره نیازمند ثبتنام است
برای مشاهده همه درسها، ویدیوها و تمرینها لطفاً ثبتنام کنید یا وارد شوید.
دوره آموزشی تابع ( فصل سوم ریاضی یازدهم تجربی )
در فصل سوم ریاضی یازدهم تجربی با توابع گویا ، وارون یک تابع و تابع یک به یک ، اعمال جبری روی توابع و … آشنا می شوید که مختصرا هر بخش رو توضیح میدیم و درون درسنامه های این دوره بصورت مفصل میتونید با مباحث این بخش آشنا بشوید…
- توابع گویا
تعریف تابع گویا
تابع رادیکالی
تابع پله ای ( تابع جزء صحیح ) - تابع یک به یک و معکوس تابع ( وارون تابع )
- اعمال جبری روی تابع
توابع گویا :
به هر تابع کسری که صورت و مخرج اون یک چندجمله ای باشه تابع گویا گفته میشه ، دقت کنید که مخرج یک تابع نباید صفر باشه و به ازای ریشه های مخرج تابع تعریف نشده است. در حالت کلی برای یک تابع کسری f(x)/g(x) دامنه کلی تابع به این صورت محاسبه میشه که ابتدا دامنه صورت کسر رو بدست میاریم و دامنه مخرج رو هم بدست میاریم و سر آخر بین دامنه های صورت و مخرج ، اشتراک میگیریم…
توابع رادیکالی :
ساده ترین تابع رادیکالی تابع y = √x است ، برای بررسی دامنه توابع رادیکالی باید دقت کنید که اگر فرجه رادیکال زوج باشد در این صورت هر آنچه که زیر رادیکال هست باید بزرگتر مساوی صفر باشه ( یعنی عبارت زیر رادیکال مثبت باشه) ولی اگه فرجه رادیکال فرد باشه مثلا فرجه ۳ باشه در این صورت وجود رادیکال محدودیتی برای رادیکال ایجاد نمی کنه.
تابع پله ای ( تابع جزء صحیح )
با یک تعریف ساده کار تابع جزء صحیح حذف ممیز و رند کردن اعداد به سمت عقب است نماد جزء صحیح به صورت [] است یعنی اگر عددی در بین این دو [] باشد باید جزء صحیح اون عدد رو محاسبه کنید ، یعنی تابع جزء صحیح همیشه ممیزها رو از بین میبره و عدد رو کوچک میکنه به مثال های زیر دقت کنید.
[۵]=۵
[۷]=۷
[۸]=۸
[-۵]=-۵
[-۹]=-۹
[-۲.۳]=-۳
[-۲.۶]=-۳
[-۲.۸]=-۳
[-۲.۸۵]=-۳
[-۲.۹۹۹]=-۳
[۴.۳]=۴
[۴.۶]=۴
[۴.۸]=۴
[۴.۸۵]=۴
[۴.۹۹۹]=۴
[۲.۳]=۲
[۲.۵]=۲
[۲.۷]=۲
[۲.۹]=۲
[۲.۹۹۹]=۲
در مثال های بالا دقت کنید که همیشه عددها کوچک تر شدند و اگر عددی بدون ممیز باشد به همان شکل از درون جزء صحیح بدون هیچ تغییری بیرون می آید.
تابع یک به یک و معکوس تابع ( وارون تابع )
تعریف تابع یک به یک به بیان ساده اینشکلی هست که به ازای هر x فقط یک y وجود داشته باشه یعنی اگه در نمودارهای تابع خطی موازی محور x ها بکشیم نمودار تابع رو فقط و فقط در یک نقطه قطع کنه ، حالا هر تابعی که یک به یک باشه وارون پذیر است و وارون تابع هم با جابجایی x وy بدست میاد ، یعنی به این صورت که ابتدا تابع رو بر حسب متغیر x مرتب می کنیم یا به اصطلاح x رو تک می کنیم…. به تصویر زیر دقت کنید.
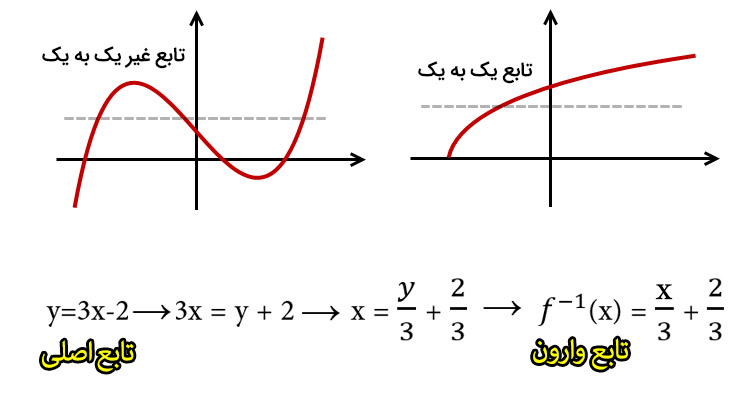
اعمال جبری روی تابع
اعمال جبری تابع یعنی پیدا کردن دامنه و ضابطه دو تابع مختلف در حالت جمع ، تفریق ، ضرب و تقسیم که در همه این حالت ها باید اشتراک دو تابع را محاسبه کرد و زمانی می توان دو تابع را جمع کرد که دامنه مشترک داشته باشند در حالت تقسیم باید توجه کنید که مخرج کسر صفر نشود و ریشه های مخرج کسر رو باید از اشتراک دامنه دو تابع کم کنید.