اول از همه باید بگم که مبحث لگاریتم بین رشته تجربی و ریاضی-فیزیک مشترک هست و به علت ساده بودن روابط این فصل معمولا برای کنکور اهمیت زیادی داره ، در ابتدا کتاب تابع نمایی رو معرفی میکنه و بعد وارد مبحث لگاریتم میشه ، کل فصل تابع نمایی و لگاریتم در قالب 8 درسنامه تدریس شده که نمونه تدریس رایگان این قسمت رو پایین همین صفحه می تونید مشاهده کنید و سر فصل های آموزشی این مبحث رو در انتهای همین صفحه ببینید.
بررسی مفهوم تابع نمایی
قبل از اینکه تابع نمایی رو معرفی کنم باید چنتا نکته ساده رو بگم که مفهوم تابع نمایی بهتر درک بشه
الف ) اگه متغیر x پایین و توان بصورت عددی بالا باشه به این مدل از روابط ، توابع چند جمله ای گفته میشه ، بصورت مثال تابع y =3x2 – 6x یک تابع چند جمله ای هست…
ب ) حالا برعکس توابع چند جمله ای اگه عدد پایین باشه و متغیر x در توان قرار داشته باشه به این مدل از روابط ، توابع نمایی گفته می شه ، بصورت مثال تابع y=2x یک تابع نمایی محسوب می شود…
توابع نمایی صعودی و نزولی را چگونه تشخیص دهیم؟
فرمول تابع نمایی در حالت کلی به صورت y = ax هست که تو این فرمول حتما حتما حتما باید a > 1 باشه و در عین حال نباید مقدار a = 1 باشه ، حالا اگه مقدار a بین صفر و یک باشه در این صورت تابع نمایی نزولی و اگه مقدار a بزرگتر از یک باشه در این صورت تابع نمایی صعودی میشه ، برای درک بهتر مطالبی که تا اینجا گفتیم به تصویر زیر دقت کنید.
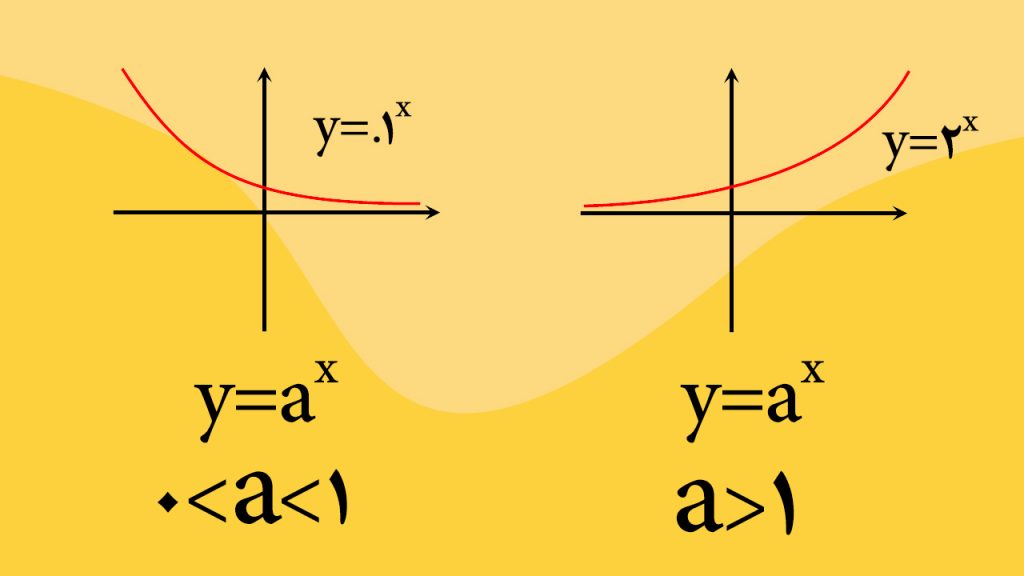
تابع لگاریتمی چگونه تعریف می شود؟
تا اینجا یاد گرفتیم که اگه پایه یک عبارت عدد و متغیر x در قسمت توان قرار داشته باشه به اون رابطه تابع نمایی گفته میشه ضمنا تو فصل تابع با مفهوم تابع وارون آشنا شدید حالا تیر خلاص رو میزنیم و تابع لگاریتمی رو تعریف می کنیم در واقع به وارون یک تابع نمایی ، تابع لگاریتمی گفته می شود. فرمول تابع لگاریتمی به صورت زیر است:
به x آرگومان لگاریتم و به a پایه یا مبنای لگاریتم گفته میشه
y = Logxa
دامنه تابع لگاریتمی چگونه محاسبه می شود؟
در رابطه y = Logxa هر دو مقدار x و a باید مثبت باشه و ضمنا a باید مخالف یک باشه و این یعنی اینکه باید برای بدست آوردن دامنه تابع لگاریتمی باید x و a رو تعیین علامت کنیم.
مثال : اگه بخواهیم دامنه y = Logx-32 رو حساب کنیم در این صورت آرگومان لگاریتم که x-3 هست رو باید بزرگتر از صفر قرار بدیم و تعیین علامت کنیم ضمنا پایه لگاریتم 2 هست که مثبت و مخالف صفر هست .
x-3>0 ⇒ x>3
خواص لگاریتم (فرمول های لگاریتم) در یک نگاه
لگاریتم ضرب رو تبدیل به جمع و تقسیم رو تبدیل به تفریق میکنه ، دقت کنید منظور ما از این حالت این هست که اگه داخل آرگومان یک لگاریتم دو عبارت در هم ضرب شوند این دو عبارت تبدیل به حاصل جمع می شود. برای اینکه فرمول های جمع و ضرب رو بهتر درک کنید به رابطه های زیر دقت کنید.
Log(x/y) = Log(x) – Log(y)
Log(x×y) = Log(x) + Log(y)
سلام عالیه عالییی ازاین تدریس هاتون خیلی رضایت دارم درکنار این تدریس هاتون کاش میشد از تدریس بی نظیر شیمی هم بهره می بردیم