برای دسترسی کامل به دوره، خریداری کنید
آموزش هندسه ( فصل دوم ریاضی یازدهم تجربی )
در فصل دوم ریاضی یازدهم تجربی بصورت خلاصه در مورد ترسیم های هندسی ، استدلال و قضیه تالس ، تشابه مثلث ها و … نکاتی رو یاد میگیریم که هر بخش رو باهم بررسی می کنیم.
- ترسیم های هندسی
- استدلال و قضیه تالس
- تشابه مثلث ها
ترسیم های هندسی
در اولین قسمت این فصل با رسم عمود منصف یک پاره خط و رسم نیمساز یک زاویه با خط کش و پرگارآشنا می شویم هر مورد رو با هم بررسی میکنیم.
رسم عمود منصف از نقطه ای خارج خط ( نقطه T و پاره خط d )
برای اینکار ابتدا از نقطه مورد نظر به کمک پرگار کمانی به اندازه AB باز می کنیم به نحوی که با خط d برخورد داشته باشد. سپس از نقاط محل برخورد A و B دو کمان به اندازه کافی بزرگ رسم میکنیم و محل برخورد دو کمان را پر رنگ میکنیم و سر آخر این دو محل برخورود رو با خط کش به هم وصل می کنیم خط رسم شده همان عمود منصف پاره خط d است.
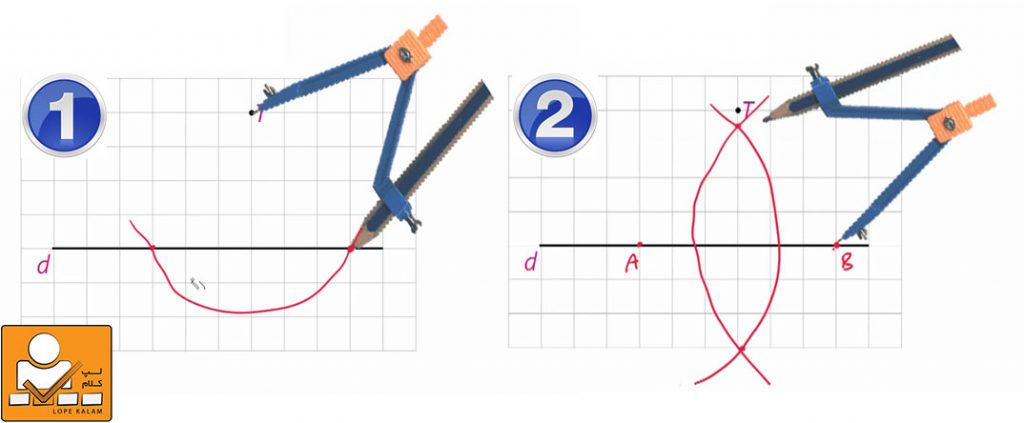
رسم نیمساز یک زاویه به کمک پرگار و خط کش
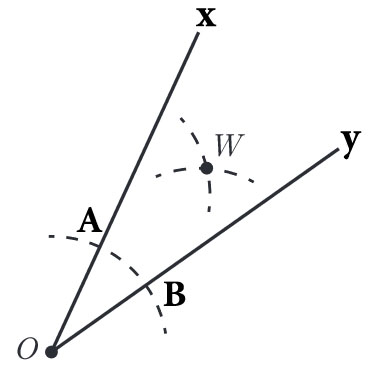
برای درک این قسمت مطابق تصویر زیر زاویه xoy رو در نظر بگیرید ابتدا به راس o یک کمان به اندازه AB باز میکنیم و سپس از نقاط A و B یک کمان دیگر باز می کنیم ، محل برخورد این دو کمان رو w نامگذاری میکنیم حالا اگه از راس o به w وصل کنیم در این صورت نیمساز زاویه xoy رسم شده است.( اثبات اینکه چرا نقطه w نیمساز زاوایه xoy است درون درسنامه اول بررسی شده است…)
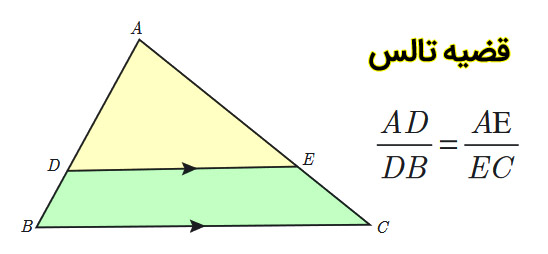
اثبات قضیه تالس :
اگر در یک مثلث خطی موازی یکی از اضلاع مثلث رسم شود ، در این صورت اضلاع آن مثلث به نسبت های مساوی تقسیم می شوند ، اثبات این قضیه به کمک استدلال استنتاجی انجام می شود و درون درسنامه های این دوره بررسی شده است.
برهان خلف و مثال نقض :
نوعی از استدلال که در اثبات های ریاضی و هندسی از آن استفاده می شود، برهان خلف نام دارد. در برهان خلف برعکس استدلال استنتاجی بجای اینکه از ابتدای مساله شروع به اثبات کنیم از حکم مساله استفاده می کنیم و یک حکم غیر صحیحی رو به عنوان فرض اولیه در نظر می گیریم و شروع به تحلیل مساله می کنیم تا جایی که به نتیجه ای برسیم که با فرض اولیه در تضاد باشد در این صورت می گوییم که فرض خلف باطل و حکم برقرار است. دقت کنید که برهان خلف برای اثبات درستی یک مساله به کار می رود ولی مثال نقض برای این استفاده میشه که نشون بدیم یک فرض از پایه غلط هست و همیشه صدق نمی کند ، بصورت مثال وقتی میگوییم که اگر هر عدد را به توان ۲ برسانیم آن عدد بزرگتر می شود به راحتی می توان این حکم رو با مثال نقض عدد ۱ رد کرد یعنی ۱ به توان ۲ برابر یک میشه و بزرگ نمیشه ( پس مثال نقض برای اثبات کردن چیزی بکار نمیره برای رد کردن حکم مساله استفاده میشه )
مثلث های متشابه :
به مثلث هایی که هر سه زاویه آنها با هم برابر است و نسبت تمامی اضلاع آنها یکسان است ، برای اثبات تشابه کافی است حالت های (ض ض ض) ، (ض ز ض) ، (ز ض ز) از دو مثلث متشابه هستند. ضمنا از اثبات مثلث های متشابه فرمول ها مهم زیر اثبات می شود.
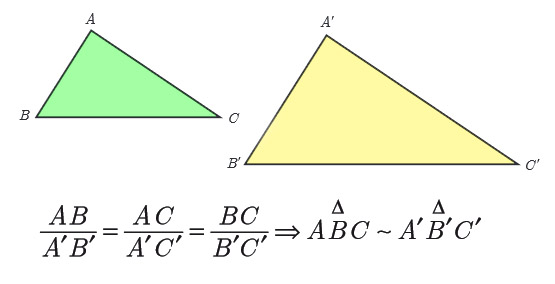
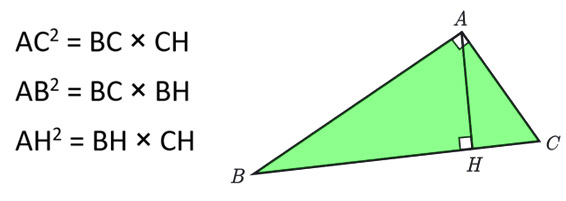
خواص خطی مثلث های قائم الزاویه :
هرگاه از راس زاویه قائمه بر روی وتر مثلث عمود رسم کنیم. در این صورت می توان روابط درون تصویر زیر رو اثبات کرد…