ریاضی یازدهم – فصل سوم

در فصل ششم ریاضی یازدهم تجربی در مورد مبحث حد و پیوستگی صحبت میشه ، مهم ترین موضوع این فصل کسرهایی هستند که بعد از جاگذاری صورت و مخرج کسرها صفر میشه و اصطلاحا به این مدل کسرها مبهم گفته می شه و باید اونهارو رفع ابهام کرد که برای رفع ابهام از تکنیک های زیر کمک می گیریم…

• رفع ابهام توابع مبهم با روش تجزیه ( ساده کردن صورت و مخرج به کمک اتحاد )
• رفع ابهام توابع رادیکالی با کمک گرفتن از روش مزدوج و یا اتحاد چاق و لاغر
• رفع ابهام به کمک توابع مثلثاتی ( بیشتر ویژه رشته ریاضی و کمی تجربی )
• رفع ابهام با روش تستی هوپیتال Hop

مفهوم حد

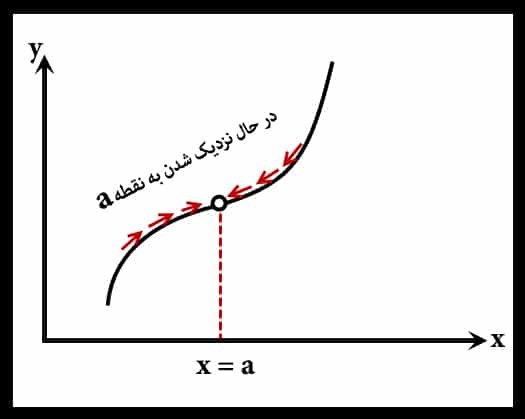
حد در یک نقطه یعنی نزدیک شدن به اون نقطه ، بصورت مثال وقتی در یک سوال گفته میشه حد تابع y=f(x) رو در نقطه مثلا x=3 حساب کنید ، معنیش این هست که مقدار تابع رو در نزدیکی نقطه ۳ یعنی بصورت مثال در ۳.۱ یا ۲.۹ بررسی کنیم ، برای درک بهتر به تصویر زیر دقت کنید تا با مفهوم حد بیشتر آشنا بشین.

بررسی مفهوم حد راست و حد چپ

حد راست عدد x=a یعنی اعداد بزرگتر از a و حد چپ یعنی اعداد کوچکتر از x=a ، فقط حواستون باشه که حد راست و حد چپ یک بازه خیلی خیلی کوچیک و نزدیک به عدد مورد نظر ما هستش ، بصورت مثال حد راست عدد ۴ می شود مثلا ۴.۱ یا مثلا ۴.۰۱ یا ۴.۰۰۱ و حد چپ عدد ۴ یعنی ۳.۹ یا مثلا ۳.۹۹ یا ۳.۹۹۹ تمامی این اعدادی که گفته شدند حد راست و حد چپ عدد ۴ به حساب می آیند به جدول زیر دقت کنید تا مفهوم حد راست ، حد چپ و حد چپ و راست رو بدرستی درک کنید. برای نشان دادن میل کردن به یک عدد از نماد → استفاده می کنند.

پیوستگی تابع در یک نقطه

اگر در یک تابع حد چپ ، حد راست و مقدار تابع در یک نقطه با هم برابر باشند در این صورت گفته میشه که تابع در یک نقطه پیوسته است یعنی

Lim f(x) = Lim f(x) = f(a)
x→a^– x→a⁺

رابطه بالا یعنی : ( حد راست = حد چپ = مقدار تابع )

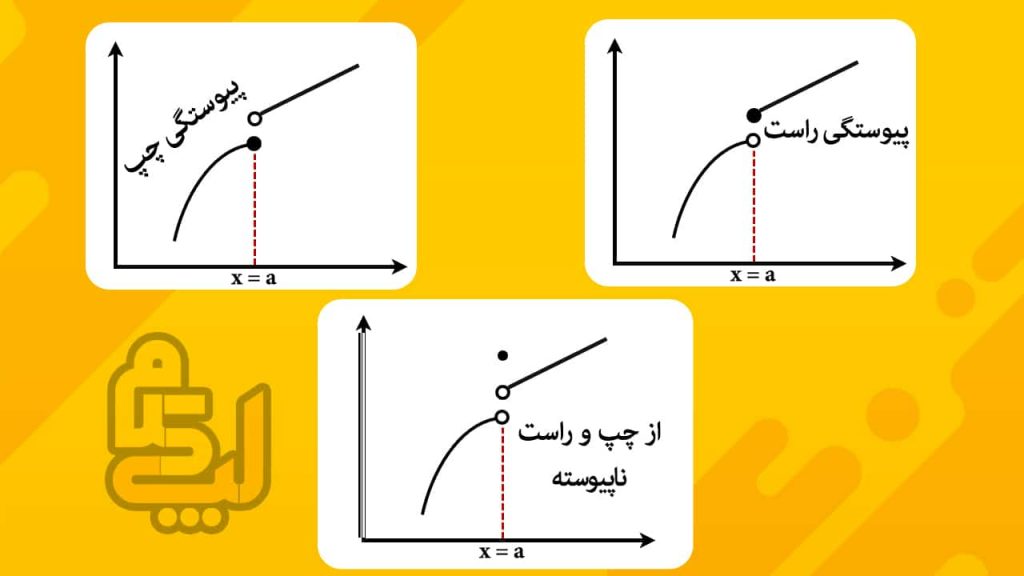
مفهوم پیوستگی راست و پیوستگی چپ در یک نقطه

اگر حد راست تابع در یک نقطه با مقدار تابع در یک نقطه برابر باشد در این صورت گفته می شود که تابع در آن نقطه پیوستگی راست دارد ولی اگر حد چپ تابع در یک نقطه با مقدار تابع در آن نقطه برابر باشد ، در این صورت گفته می شود که تابع در آن نقطه پیوستگی چپ دارد. ضمنا اگر هیچ کدام از مقادیر حد چپ و حد راست تابع با مقدار تابع برابر نباشد در این صورت گفته می شود که تابع نه پیوستگی راست دارد و نه پیوستگی چپ .

برای درک بهتر مفهوم پیوستگی راست و پیوستگی چپ به تصویر زیر دقت کنید.

توجه : مقدار تابع در نمودارها با یک نقطه تو پر نمایش داده می شود.

رفع ابهام توابع صفر صفرم ( توابع مبهم )

وقتی در محاسبه یک حد Lim f(x) زمانی که x→a میل می کند به جواب ۰/۰ برسیم . در این حالت گفته می شود که حد تابع f(x) در نقطه x=a مبهم است و باید رفع ابهام شود ، رفع ابهام یعنی عواملی که باعث می شوند صورت و مخرج صفر شود رو حذف کنیم.

⭐ برای رفع ابهام توابع چند جمله ای از اتحادهای جمله مشترک ، اتحاد مربع و … کمک میگیریم.
⭐ برای رفع ابهام توابع رادیکالی با فرجه ۲ از اتحاد مزدوج برای رفع ابهام حالت صفر صفرم
کمک می گیریم.
⭐ برای رفع ابهام توابع رادیکالی با فرجه ۳ از اتحاد چاق و لاغر برای از بین بردن حالت صفر صفرم
کمک می گیریم.
⭐ برای رفع ابهام توابع مثلثاتی از اتحادهای مثلثاتی کمک می گیریم.
⭐ برای رفع ابهام اکثر توابع میشه از روش تستی و ویژه هوپیتال Hop استفاده کرد . 😊🧡