در این درسنامه به بحث و بررسی بر روی دنباله حسابی پرداخته می شود . یک دنباله زمانی می تواند دنباله حسابی محسوب شود که که تمام جملات آن با نسبت خاصی زیاد شود. بطور مثال هر جمله آن نسبت به جمله قبلی خود به علاوه عدد خاصی شود. بصورت مثال اعداد زیر نماینده یک دنباله حسابی هستند
8 , 10 , 12 , 14 , 16 , …. ====> هر جمله به علاوه عدد 2 شده است
3 , 7 , 11 , 15 , 19 , …. ====> هر جمله به علاوه عدد 4 شده است
-10 , -15 , -20 , -25 , -30 , -35 , …. ====> هر جمله منهای عدد 5 شده است
بنابراین طبق الگوی بالا هر جمله نسبت به جمله قبلی خود در دنباله حسابی باید به اندازه یک عدد یکسان کم و یا جمع شود. در غیر این صورت دنباله حسابی محسوب نخواهد شد و اما فرمول محاسبه دنباله حسابی بصورت زیر است.
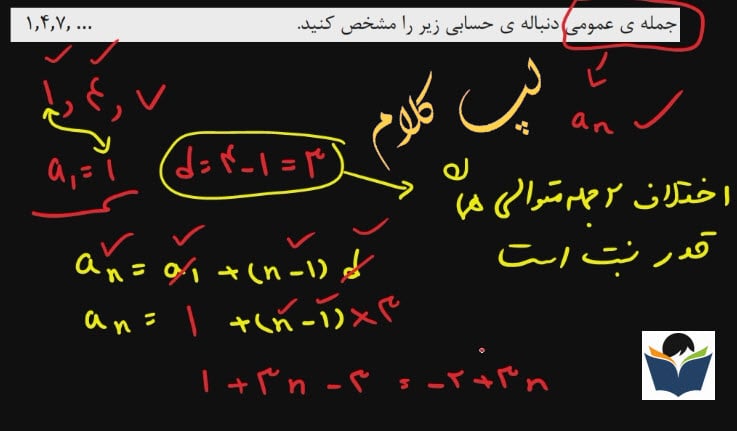
an= a1 + (n-1) d
که در این فرمول هر کدام از اجزای این فرمول نامی مشخص برای خود دارند.
an : جمله عمومی
a1 : جمله اول
n : شماره جمله ، تعداد جمله ، ….
d : قدر نسبت دنباله حسابی
به یک مثال ساده توجه کنید.
در یک دنباله حسابی جمله اول این دنباله برابر 17 و قدر نسبت این دنباله 3 است .
الف ) جمله 51 ام این دنباله را بدست آورید.
ب ) جمله عمومی این دنباله را بدست آورید.
راه حل مساله قسمت الف )
an= a1 + (n-1) d
an= 17 + (n-1) * 3 = 17 + 3n -3 = 14 + 2n
راه حل مساله قسمت ب)
در این قسمت کافی است که هر جایی مقدار n دیدیم بجای آن مقدار 51 قرار داده و فرمول را ساده کنیم
an= a1 + (n-1) d
an= 17 + (n-1) * 3
an= 17 + (51-1) * 3 = 17 + 50 * 3 = 17 + 150 = 167
کافی است که بجای مقدار n مقدار 51 قرار دهیم و بعد از آن دنباله حسابی خواسته شده را ساده کنیم.
اگر آنچه که در بالا گفته شده برای شما گیج کننده است کافی است که درسنامه تصویری مربوط به دنباله حسابی را مشاهده کنید تا در عرض چند دقیقه کوتاه به تسلط کافی بر روی این مبحث دست پیدا کنید.
برای دانلود درسنامه فوق کافی است که بر روی << اینجا >> کلیک کنید.


بسیار عالی.
خیلی ممنون