ریاضی دوم دبیرستان – درسنامه اول – دنباله ها

آموزش ریاضی دوم دبیرستان – مبحث دنباله ها

مباحث مقدماتی دنباله ها

همانطور که می دانید فصل اول ریاضی دوم دبیرستان با مبحث دنباله ها آغاز می شود. در حالت کلی مباحث این فصل را می توان به سه دسته کلی تقسیم کرد

• دنباله های حسابی
• دنباله های هندسی
• دنباله های غیر هندسی و غیر حسابی

یعنی با توجه به تعریف کتاب درسی می توان بی نهایت دنباله تعریف کرد ولی از این میان ، دو دسته از دنباله ها اهمیت زیادی دارند که  نامی خاص برای آنها در نظر گرفته شده است ( حسابی و هندسی )

 

 

برای آنکه یک دنباله تعریف شود کافی است که اعداد ورودی یک تابع مانند ( F ( x جزو اعداد طبیعی باشند بنابراین اعدادی مثل 1.4 و 1/3 و 30 – و …. به عنوان ورودی نمی توانند در نظر گرفته شوند .

یاد آوری اعداد طبیعی : اعداد طبیعی اعدادی هستند که با آنها شمارش صورت می گیرد مانند زیر :

N = { 1 , 2 , 3 , 4 , 5 , 6 , …. }

مثال

چند جمله اول دنباله های زیر را مشخص کنید.

a_n= 1/n  ===> {1/1 , 1/2 , 1/3 , 1/4 , 1/5 , …..}

a_n= 2/n ===> { 2/1 , 2/2 , 3/2 , 4/2 , 5/2 , 6/2 , ….}

a_n= n²  ===> { 1^2 , 2^2 , 3^2 , 4^2 , 5^2 , 6^2 , …. }

بنابراین آنچه که در محاسبه جملات یک دنباله اهمیت دارد این است که اعداد طبیعی درون آن قرار گیرند .یعنی برای حل سه مثال فوق کافی بود به جای n درون هر دنباله اعداد طبیعی قرار میگرفت ولی اگر اندیس یک دنباله به جای آنکه n باشد عبارتی غیر از n باشد ( مانند 2n , 2n-1 ) در این صورت روند حل مساله کمی فرق می کرد که بخاطر پیچیدگی روند حل این نوع مسایل  مثال های مربوط به این گونه سوالات را در درسنامه تصویری مشاهده کنید.

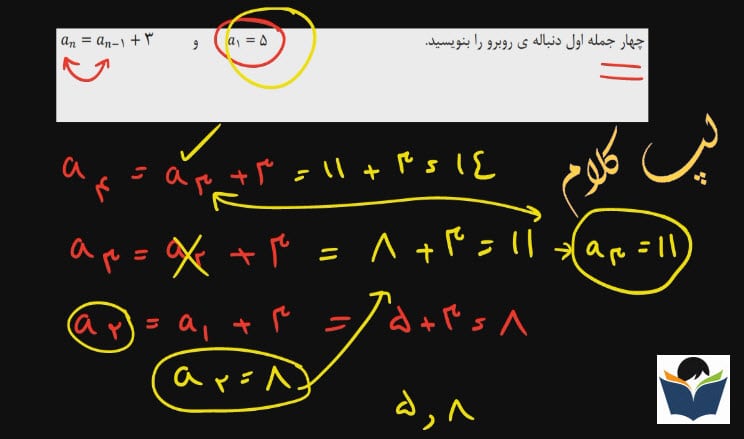
غیر از آنچه که در بالا مطرح شد در بعضی از  سوالات هر جمله به جملات قبلی خود وابسته هستند که این دسته از سوالات به  دنباله های بازگشتی معروف هستند یعنی برای محاسبه هر جمله به جمله قبلی نیاز است

برای یادگیری نکات بیشتر و تسلط بر روی آنچه در بالا گفته شد کافی است که ویدئوی آموزشی مربوط به درسنامه اول را در زیر مشاهده کنید

برای دانلود این درسنامه کافی است بر روی << اینجا >> کلیک کنید.