✍شرط همواره مثبت و همواره منفی معادله درجه دوم

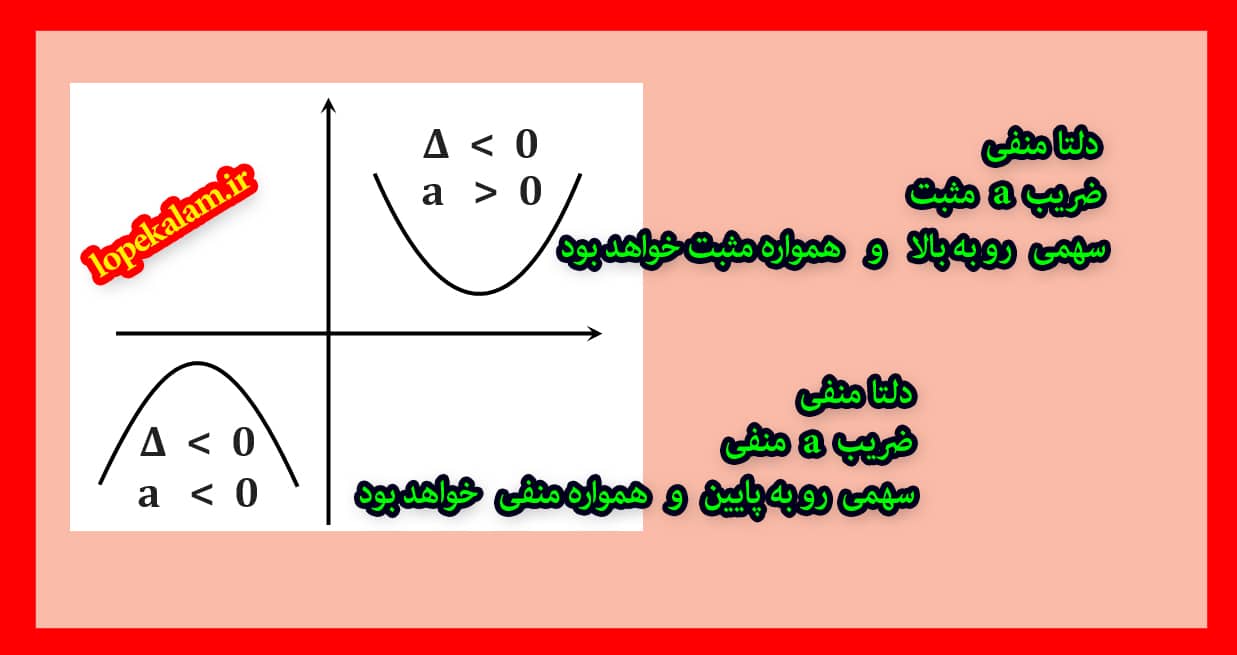
عبارت های همواره مثبت یا عبارت های همواره منفی عبارت هایی هستند که همواره بالای محور ایکس و یا همواره زیر محور ایکس هستند بنابراین y یعنی برد آنها همیشه مثبت یا همیشه منفی هست ، پس عبارت های همواره مثبت یا همواره منفی هرگز هرگز ریشه ندارند ، خب نتیجه مهم تری که این وسط میشه گرفت این هستش که دلتای عبارت های همواره مثبت و همواره منفی همیشه همیشه همیشه منفی خواهد بود. خوب حالا چجوری تشخیص بدیم که سهمی ما رو بالا هست یا رو به پایین هست ؟ کافیه که به ضریب a  دقت کنین ، اگر ضریب a مثبت باشه سهمی رو به بالا و اگه ضریب a  منفی باشه سهمی رو به پایین میشه.

شرط همواره مثبت بودن معادله درجه دوم

شرط همواره مثبت بودن معادله درجه دوم دو چیز هست :
۱- دلتای معادله درجه دوم منفی باشه
۲- ضریب x^۲ یعنی a مثبت باشه

به صورت مثال معادله درجه دوم y=2x^۲ – 3x +5 همواره مثبت هست ، چرا؟ خب کافیه ۲ تا شرط بالا رو بررسی کنیم.
۱- شرط دلتا

Δ = b^۲ – 4ac = (-3)^۲ – ۴ × ۲ × ۵ = 9 – ۴۰ = -۳۱

خب تا اینجا شرط اول برقراره یعنی دلتای معادله درجه دوم منفی شد و اما بررسی شرط دوم که خیلی آسون تره ، تو شرط دوم کافیه که به ضریب x^۲ نگاه کنیم ، که تو این معادله عدد ۲x^۲ هست که کاملا مشخصه عدد ۲ مثبت و بزرگتر از صفره پس عبارت ما همواره مثبت هست.

شرط همواره منفی بودن معادله درجه دوم

شرط همواره منفی بودن هم دو چیز هست :
۱- دلتای معادله درجه دوم منفی باشه
۲- ضریب x^۲ یعنی a منفی باشه
مثال : ثابت کنید که معادله درجه دوم y= -1x^۲ + 4x – 6 همواره منفی است.
باز هم باید دو شرط رو بررسی کنیم :
۱- شرط دلتا
خب اول از همه باید چک کنیم که دلتای عبارت درجه دوم منفی باشه پس برسیم سراغ دلتا :

Δ = b^۲ – 4ac = ( 4 )^۲ – ۴ × (-۱) × (-۶) = 16 – ۲۴ = -۸

خب تا اینجا دلتای معادله درجه دوم منفی شده پس میریم سراغ ضریب معادله درجه دوم یعنی ۱x^۲– که ۱- هست و مشخصه که این ضریب هم منفی هستش بنابراین ، دو شرط ما برقراره و معادله درجه دوم همواره منفی هست.

حذف عبارت های همواره مثبت از تعیین علامت

نکته : در هنگام تعیین علامت عبارت های جبری برای ساده سازی و افزایش سرعت عمل میشه عبارت های همواره مثبت رو حذف کرد و این قضیه یعنی حذف عبارت های همواره مثبت هیچ تاثیری در جواب نهایی تعیین علامت نداره ، پس با خیال راحت هنگام تعیین علامت ، عبارت های همواره مثبت رو حذف کنید.

مثال : به ازای چه مقادیری از a عبارت  y = 2 x^۲ + ۴ x + a   همواره مثبت است ؟

y = 2 x^۲ + ۴ x + a

Δ = b^۲ – ۴ac =4^۲ – ۴(۲)(a) > 0   =>  ۱۶ – ۸a > 0   =>  ۸a < 16   =>  a <  ۲

فقط حواستون باشه همیشه ضریب ایکس به توان ۲ رو چک کنین و اگه لازم شد با جواب دلتا اشتراک بگیرین ، بصورت مثال توی سوال بالا ضریب a ، عدد ۲ هستش که مثبت هستش و نیازی به اشتراک گیری نداره ، برای درک بهتر به ویدیوی این قسمت مراجعه کنید…