بسیار مهم بسیار مهم قبل از بررسی معادلات مثلثاتی
اگر درسنامه های قبلی را نگاه نکرده اید حتما آنها را نگاه کرده تا به معجزه گر بودن دایره مثلثاتی در حل معادلات مثلثاتی پی ببرید وگرنه در فهم این درسنامه به مشکل بر خواهید خورد.
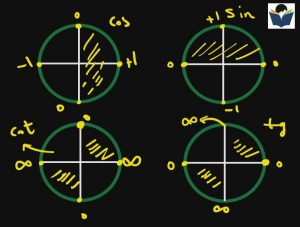
در جلسه های قبل بررسی مثلثات به بحث و بررسی بر روی دایره مثلثاتی و مثال هایی از آن پرداخته شد هر چه قدر با این دایره مثلثاتی بیشتر کار کنید کارا بودن و کاربردی بودن آن را بیشتر درک خواهید کرد . در جلسه پنجم قصد حل کردن معادلات مثلثاتی و بررسی روابط kπ است. قبل از آنکه معادلات مثلثاتی را بررسی کنیم بطور خلاصه یاد آوری می شود ناحیه مثبت sin در ربع ۱ و ۲ بود
ناحیه مثبت cos در ربع ۱ و ۴ بود
ناحیه مثبت tan در ربع ۱ و ۳ بود
ناحیه مثبت cot در ربع ۱ و۳ بود
همانطور که در درسنامه های قبلی بررسی شد حفظ ناحیه ها بصورت فوق کار سختی است بجای آن از حافظه تصویری خود استفاده کنید و تصویر ساده زیر را بخاطر بسپارید که بسیار کار آسان تری است.
اگر تصویر فوق برایتان معنای خاصی ندارد به معنای آن است که درسنامه های قبلی رانگاه نکرده اید و یا در حافظه بلند مدت اتان قرار نگرفته است اکیدا توصیه می کنم که حتما سری به درسنامه های قبلی زده و آنها را مرور کنید .
لینک درسنامه های قبلی
و اما روابط Kπ
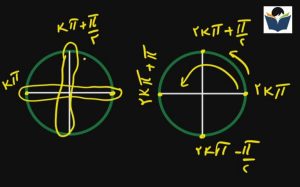
روابطی که کتاب درسی برای حل معادلات مثلثاتی مطرح کرده است بسیار زیاد و عموما نامفهوم است ولی با دایره های مثلثاتی گفته در درسنامه های قبلی نه تنها پیچیده نیست بلکه بسیار راحت و شیرین خواهد شد . خلاصه درسنامه قبلی در مبحث روابط Kπ به این نتیجه خواهد رسید که نقاط زوج ( سمت راست ) نقطه 2kπ خواهد بود
و نقاط سمت چپ ۲/ 2kπ + π خواهد شد. و همینطور نقاط بالا و پایین
بهتر است بجای طولانی کردن روابط از حافظه تصویری خودتان استفاده کنید و کلیه مطالب را در شکل ساده زیر مشاهده کنید.
۲ تصویر فوق را حتما دانلود کرده و یا در دفتر خود کشیده و در حل معادلات مثلثاتی به آنها رجوع کرده تا در حافظه بلند مدت شما قرار گیرد .
به حل یک معادله مثلثاتی با روابط گفته شده دقت کنید .
معادله مثلثاتی زیر را حل کنید.
sin^2 ( x ) + 5 * sin ( x ) – 6 = 0
ابتدا دقت شود معادله فوق یک معادله درجه دوم است با روش دلتا و یا هر روش دیگری متوجه می شویم جواب معادله به صورت زیر در می آید . ( اگر با حل معادله فوق مشکل دارید به فایل تصویری این درسنامه که در پایین همین صفحه آمده است مراجعه شود )
Sin( x ) = 1
Sin( x ) = -6
از دو جواب فوق تنها عبارت Sin( x ) = 1 مورد قبول است زیرا سینوس محدود به اعداد بین صفر و یک است و عددی خارج از این بازه نمی تواند داشته باشد بنابراین عبارت Sin( x ) = -6 قابل پذیرش نیست. جواب کلی این معادله مثلثاتی بر حسب روابط Kπ بصورت x= 2kπ +π/۲ خواهد شد.
اگر آنچه در بالا گفته شد برای شما نامفهوم است به شما حق می دهم . برای شفاف شدن مطالب گفته شده و درک بهتر روابط مثلثاتی و تسلط بر روی مبحث معادلات مثلثاتی که یکی از پر تست خیز ترین مباحث کنکور است کافی است فایل تصویری زیر را مشاهده کنید
برای دانلود درسنامه فوق کافی است بر روی << اینجا >> کلیک کنید

سلام توضیحات مثلثات فوقالعاده بود تروخدا زودتر بقیشم بذارین
سلام خيلي ممنون ،من از اون دسته آدماي تماشاچى هستم ولي نتونستم ازتون تشكر نكنم از زحماتتون قدردانم ،در ضمن من بعد از سالها دوباره مى خوام در كنكور شركت كنم و خيلي وب سايت مفيدي بود خوشحالم پيداش كردم و هميشه تب اين صفحه را باز مى گذارم اگر مى شد مثلثات رو بازم ادامه بدين ممنون ميشم
سلام مثلثات خیلی از مباحثش ناقص مونده که باید ادامه بدم ولی احتمالا می مونه بعد عید فعلا درگیر کارهای دیگه هستم