یکی از مباحث مهم کتاب ریاضی دوازدهم (حسابان دوازدهم ) مبحث مشتق است ، دانش آموزان در این فصل باید مشتق توابع چند جمله ای ، مشتق توابع کسری ، مشتق توابع رادیکالی ، مشتق توابع ضربی ، مشتق توابع fog و … را بخوبی یاد بگیرند ، که در این پست کوتاه می خواهیم با همدیگه مشتق توابع رادیکلی رو خیلی سریع و حرفه ای بررسی کنیم.
مشتق تابع y = √x
قبل از اینکه فرمول مشتق توابع رادیکالی رو معرفی کنیم ، بهتره که ساده ترین نوع مشتق تابع رادیکالی رو حفظ کنید که فرمول اون رو در زیر می بینید.
فرمول مشتق رادیکال x رو این شکلی حفظ کنید که میشه : 1 بر روی 2 رادیکال x
مشتق توابع رادیکالی در حالت کلی چگونه محاسبه می شود؟
فرمول مشتق تابع رادیکالی در حالت کلی چندتا مرحله داره که همین ابتدا توصیه میکنم ویدئوی مربوط به این بخش رو پایین همین صفحه نگاه کنید چون کمی مراحلش طولانیه و اما به هر کدوم یکی یکی اشاره می کنیم .
گام اول : برای حل مشتق تابع رادیکالی اول از همه به فرجه رادیکال باید دقت بشه که فرجه 2 یا 3 یا در حالت کلی چه عددی هست گام دوم : بعد از اون سریعا یک خط کسری بکشید و در مخرج کسر یک رادیکال بنویسید و فرجه رو در پشت رادیکال به عنوان ضریب ، و همچنین به عنوان فرجه بنویسید.
گام سوم : تو مرحله بعدی توان فرجه رو از توان رادیکال کم کنید.
گام چهارم : سر آخر در صورت کسر بدون در نظر گرفتن توان از عبارت زیر رادیکال مشتق بگیرید. اگه نکاتی که در بالا گفتیم رو بدرستی پیاده سازی کنیم به فرمول زیر می رسیم…
حل چند مثال از مشتق توابع رادیکالی
مثال 1: مشتق تابع زیر را محاسبه کنید.
گام اول : برای حل سوال بالا اول از همه باید یک خط کسری بکشیم و در زیر خط کسری یک رادیکال با فرجه و ضریب 3 بنویسیم ( چرا ؟ به خاطر اینکه در صورت سوال مشتق تابع رادیکالی با فرجه 3 داده شده ) یعنی تا اینجای کار فرمول ما به صورت زیر در میاد:
گام دوم : در مرحله بعدی عبارت زیر رادیکال رو در مخرج کسر نوشته و توان عبارت زیر رادیکال رو از فرجه کم می کنیم پس به این ترتیب فرمول ما به صورت زیر در میاد و دیگه کاری با مخرج کسر نداریم.
گام سوم : در مرحله آخر ، توان عبارت زیر رادیکال رو در صورت کسر می نویسیم و سپس بدون در نظر گرفتن این توان از عبارت زیر اون مشتق می گیریم.
مثال 2: مشتق تابع رادیکالی روبرو را بدست آورید. ( ساده سازی لازم نیست )
گام اول: همانند سوال قبلی ابتدا یک خط کسری بکشید و در مخرج کسر ، یک رادیکال با فرجه و ضریب 5 بنویسید.
گام دوم: در مرحله بعدی عبارت زیر رادیکال رو در مخرج کسر نوشته و توان اون رو از فرجه کم کنید.
( تا اینجا اگه درست نوشته باشین باید به جواب زیر رسیده باشین ، خوب به مراحل سوال دقت کنید تا به سادگی بتونید سوالات این بخش رو حل کنید)
گام سوم: و اما در مرحله آخر دیگه کاری با مخرج کسر نداریم و نوبتی هم که باشه نوبت صورت کسر هستش که گاهی دانش آموزان تو این مرحله دچار خطای محاسباتی میشن ، همیشه دقت کنید که تو این مرحله اول از همه توان عبارت زیر رادیکال رو می نویسم و دیگه با این توان کاری نداریم و بدون در نظر گرفتن این توان از هر عبارتی که باقی موند مشتق می گیریم ، پس اگه با دقت این کارو انجام بدیم جواب نهایی به صورت زیر در میاد:


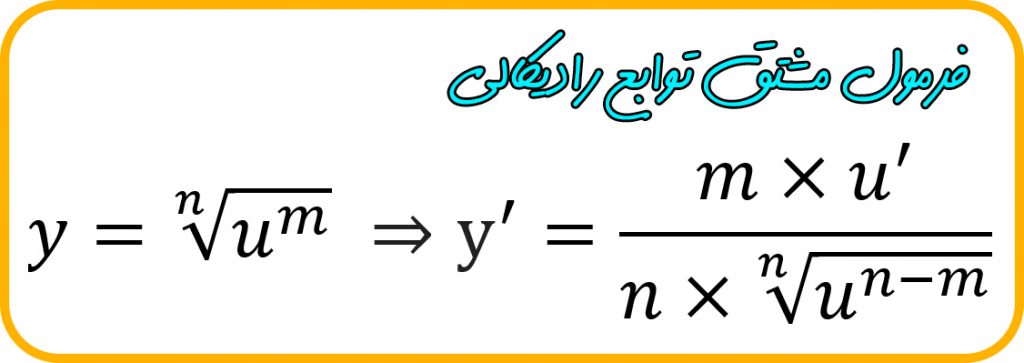
عالییییییی…????????????????????????????????